Community detection in hypergraphs via mutual information maximization
- PMID: 38521798
- PMCID: PMC10960844
- DOI: 10.1038/s41598-024-55934-5
Community detection in hypergraphs via mutual information maximization
Abstract
The hypergraph community detection problem seeks to identify groups of related vertices in hypergraph data. We propose an information-theoretic hypergraph community detection algorithm which compresses the observed data in terms of community labels and community-edge intersections. This algorithm can also be viewed as maximum-likelihood inference in a degree-corrected microcanonical stochastic blockmodel. We perform the compression/inference step via simulated annealing. Unlike several recent algorithms based on canonical models, our microcanonical algorithm does not require inference of statistical parameters such as vertex degrees or pairwise group connection rates. Through synthetic experiments, we find that our algorithm succeeds down to recently-conjectured thresholds for sparse random hypergraphs. We also find competitive performance in cluster recovery tasks on several hypergraph data sets.
© 2024. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures



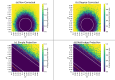







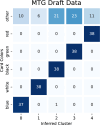
References
-
- Newman M. Networks: An Introduction. Oxford University Press; 2018.
-
- Bick C, Gross E, Harrington HA, Schaub MT. What are higher-order networks? SIAM Rev. 2023;65:686–731. doi: 10.1137/21M1414024. - DOI
-
- Torres L, Blevins AS, Bassett D, Eliassi-Rad T. The why, how, and when of representations for complex systems. SIAM Rev. 2021;63:435–485. doi: 10.1137/20M1355896. - DOI
-
- Ke, Z. T., Shi, F. & Xia, D. Community detection for hypergraph networks via regularized tensor power iteration. arXiv:1909.06503 (2019).
Grants and funding
LinkOut - more resources
Full Text Sources

