Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2023 Jul 20;51(5):1007-1022.
doi: 10.1080/02664763.2023.2229973. eCollection 2024.

Alternative statistical modeling for radical prostatectomy data

Julio C S Vasconcelos  1 , Thiago da Costa Travassos  2 , Edwin M M Ortega  3 , Gauss M Cordeiro  4 , Leonardo Oliveira Reis  5
Affiliations

Alternative statistical modeling for radical prostatectomy data

Julio C S Vasconcelos et al. J Appl Stat. .

Abstract

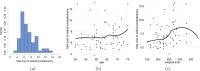
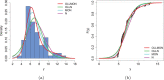
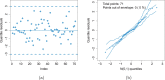
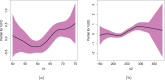
Several statistical models have been proposed in recent years, among them is the semiparametric regression. In medicine, there are several situations in which it is impracticable to consider a linear regression for statistical modeling, especially when the data contain explanatory variables that present a nonlinear relationship with the response variable. Another common situation is when the response variable does not have a unimodal shape, and it is not possible to adopt distributions belonging to the symmetric or asymmetric classes. In this context, a semiparametric heteroskedastic regression is proposed based on an extension of the normal distribution. Then, we show the usefulness of this model to analyze the cost of prostate cancer surgery. The predictor variables refer to two groups of patients such that one group receives a multimodal local anesthetic solution (Preemptive Target Anesthetic Solution) and the second group is treated with neuraxial blockade (spinal anesthesia/traditional standard). The other relevant predictor variables are also evaluated, thus allowing for the in-depth interpretation of the predictor variables with a nonlinear effect on the dependent variable cost. The penalized maximum likelihood method is adopted to estimate the model parameters. The new regression is a useful statistical tool for analyzing medical data.

Keywords: 62-08; 62-11; 62P10; Cubic smoothing splines; Marshall-Olkin family; local anesthetic; prostate cancer; quantile residuals.

PubMed Disclaimer

Conflict of interest statement

No potential conflict of interest was reported by the author(s).

Figures

Figure 1.
Figure 1.
(a) Histogram of the cost of open radical prostatectomy (divided by 1000). (b) Dispersion plot of the cost of open radical prostatectomy versus patient age (in years). (c) Dispersion plot of the cost of open radical prostatectomy versus duration (in minutes) of the operation.
Figure 2.
Figure 2.
True and estimated curves for the smooth function h(ti1): (a) n = 60, (b) n = 180, (c) 360 and (d) 540.
Figure 3.
Figure 3.
Normal probability plots for the qrs with sample sizes: (a) n = 60, (b) n = 180, (c) 360 and(d) 540.
Figure 4.
Figure 4.
(a) Estimated densities to prostatectomy data. (b) Estimated cdfs.
Figure 5.
Figure 5.
(a) Plot of the qrs versus the index. (b) Normal probability plot for the qrs with envelope.
Figure 6.
Figure 6.
Estimated smooth curve. (a) Age (in years). (b) Surgical time (in minutes).
Figure A1.
Figure A1.
(a) Plots of the Bowleys skewness as function of ν and τ for μ=0.01 and σ=1. (b) Plots of the Moors' kurtosis as function of ν and τ for μ=0.5 and σ=3.
See this image and copyright information in PMC

References

    1. Atkinson A.C., Plots, Transformations and Regression; An Introduction to Graphical Methods of Diagnostic Regression Analysis, Clarendon Press Oxford, Oxford, 1985.
    1. Cardozo C.A., Paula G.A., and Venegas L.H., Generalized log-gamma additive partial linear models with P-spline smoothing, Stat. Papers 63 (2022), pp. 1953–1978.
    1. Chou R., Gordon D.B., de Leon-Casasola O.A., Rosenberg Ja.M., Bickler S., Brennan T., Carter. C.L. Cassidy T., Chittenden E.H., Degenhardt E., Griffith S., Manworren R., McCarberg B., Montgomery R., Murphy J., Perkal M.F., Suresh S., Sluka K., Strassels S., Thirlby R., Viscusi E., Walco G.A., Warner L., Weisman S.J., and Wu C.L., Management of postoperative pain: A clinical practice guideline from the American pain society, the American society of regional anesthesia and pain medicine, and the American society of anesthesiologists committee on regional anesthesia, executive committee, and administrative council, J. Pain 17 (2016), pp. 131–157. - PubMed
    1. da Silva Braga A., Cordeiro G.M., Ortega E.M., and da Cruz J.N., The odd log-logistic normal distribution: Theory and applications in analysis of experiments, J. Stat. Theory. Pract. 10 (2016), pp. 311–335.
    1. Dunn P.K. and Smyth G.K., Randomized quantile residuals, J. Comput. Graph. Stat. 5 (1996), pp. 236–244.

LinkOut - more resources