High-threshold and low-overhead fault-tolerant quantum memory

Abstract

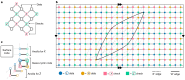
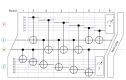
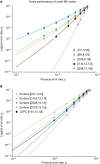
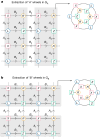
The accumulation of physical errors^1-3 prevents the execution of large-scale algorithms in current quantum computers. Quantum error correction⁴ promises a solution by encoding k logical qubits onto a larger number n of physical qubits, such that the physical errors are suppressed enough to allow running a desired computation with tolerable fidelity. Quantum error correction becomes practically realizable once the physical error rate is below a threshold value that depends on the choice of quantum code, syndrome measurement circuit and decoding algorithm⁵. We present an end-to-end quantum error correction protocol that implements fault-tolerant memory on the basis of a family of low-density parity-check codes⁶. Our approach achieves an error threshold of 0.7% for the standard circuit-based noise model, on par with the surface code^7-10 that for 20 years was the leading code in terms of error threshold. The syndrome measurement cycle for a length-n code in our family requires n ancillary qubits and a depth-8 circuit with CNOT gates, qubit initializations and measurements. The required qubit connectivity is a degree-6 graph composed of two edge-disjoint planar subgraphs. In particular, we show that 12 logical qubits can be preserved for nearly 1 million syndrome cycles using 288 physical qubits in total, assuming the physical error rate of 0.1%, whereas the surface code would require nearly 3,000 physical qubits to achieve said performance. Our findings bring demonstrations of a low-overhead fault-tolerant quantum memory within the reach of near-term quantum processors.

Fig. 1. Tanner graphs of surface and BB codes.

a, Tanner graph of a surface code, for comparison. b, Tanner graph of a BB code with parameters [[144, 12, 12]] embedded into a torus. Any edge of the Tanner graph connects a data and a check vertex. Data qubits associated with the registers q(L) and q(R) are shown by blue and orange circles. Each vertex has six incident edges including four short-range edges (pointing north, south, east and west) and two long-range edges. We only show a few long-range edges to avoid clutter. Dashed and solid edges indicate two planar subgraphs spanning the Tanner graph, see the Methods. c, Sketch of a Tanner graph extension for measuring $\overline{Z}$ and $\overline{X}$ following ref. , attaching to a surface code. The ancilla corresponding to the $\overline{X}$ measurement can be connected to a surface code, enabling load-store operations for all logical qubits by means of quantum teleportation and some logical unitaries. This extended Tanner graph also has an implementation in a thickness-2 architecture through the A and B edges (Methods).

Fig. 2. Syndrome measurement circuit.

Full cycle of syndrome measurements relying on seven layers of CNOTs. We provide a local view of the circuit that only includes one data qubit from each register q(L) and q(R). The circuit is symmetric under horizontal and vertical shifts of the Tanner graph. Each data qubit is coupled by CNOTs with three X-check and three Z-check qubits: see the Methods for more details.

Fig. 3. Noise properties of BB codes.

a, Logical versus physical error rate for small examples of BB LDPC codes. A numerical estimate of p_L (diamonds) was obtained by simulating d syndrome cycles for a distance-d code. Most of the data points have error bars roughly equal to p_L/10 due to sampling errors. b, Comparison between the BB LDPC code [[144, 12, 12]] and surface codes with 12 logical qubits and distance d ∈ {9, 11, 13, 15}. The distance-d surface code with 12 logical qubits has the length n = 12d² because each logical qubit is encoded into a separate d × d patch of the surface code lattice.

Extended Data Fig. 1. Decomposition of the Tanner graph into planar graphs.

Two different grids over a torus defined using different subsets of A₁, A₂, A₃, B₁, B₂, B₃. Edge labels indicate adjacency matrices that generate the respective edges. By extracting either horizontal or vertical strips from these grids, we obtain planar ‘wheel graphs’ whose union contains all edges in the Tanner graph. To avoid clutter, each grid shows only a subset of edges present in the Tanner graph. a, The A wheels (dashed lines) cover A₂, A₃, B₃. b, The B wheels (solid lines) cover B₁, B₂, A₁.

Extended Data Fig. 2. Navigating the Tanner graph.

a, A ‘compass’ diagram that shows the direction in which matrices A and B are applied to travel between different nodes. b, The unit cell of the construction of a toric layout in the proof of Lemma 4.