Enhancing the Spin Hall Effect of Cylindrically Polarized Beams
- PMID: 38542597
- PMCID: PMC10971798
- DOI: 10.3390/mi15030350
Enhancing the Spin Hall Effect of Cylindrically Polarized Beams
Abstract
Two linked gear wheels in a micromachine can be simultaneously rotated in opposite directions by using a laser beam that has in its section areas the spin angular momentum (SAM) of the opposite sign. However, for instance, a cylindrical vector beam has zero SAM in the focus. We alter a cylindrical vector beam so as to generate areas in its focus where the SAM is of opposite signs. The first alteration is adding to the cylindrical vector beam a linearly polarized beam. Thus, we study superposition of two rotationally symmetric beams: those with cylindrical and linear polarization. We obtain an expression for the SAM and prove two of its properties. The first property is that changing superposition coefficients does not change the shape of the SAM density distribution, whereas the intensity changes. The second property is that maximal SAM density is achieved when both beams in the superposition have the same energy. The second perturbation is adding a spatial carrier frequency. We study the SAM density of a cylindrical vector beam with a spatial carrier frequency. Due to periodic modulation, upon propagation in space, such a beam is split into two beams, having left and right elliptic polarization. Thus, in the beam transverse section, areas with the spin of different signs are separated in space, which is a manifestation of the spin Hall effect. We demonstrate that such light beams can be generated by metasurfaces, with the transmittance depending periodically on one coordinate.
Keywords: beam energy; carrier frequency; cylindrical vector beam; spin Hall effect; spin angular momentum.
Conflict of interest statement
The authors declare no conflicts of interest. The funders had no role in the design of the study, the collection, analysis, or interpretation of data, the writing of the manuscript, or the decision to publish the results.
Figures


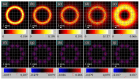





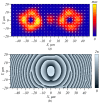
Similar articles
-
Spin Hall Effect in the Paraxial Light Beams with Multiple Polarization Singularities.Micromachines (Basel). 2023 Mar 30;14(4):777. doi: 10.3390/mi14040777. Micromachines (Basel). 2023. PMID: 37421010 Free PMC article.
-
Spin Hall Effect of Double-Index Cylindrical Vector Beams in a Tight Focus.Micromachines (Basel). 2023 Feb 20;14(2):494. doi: 10.3390/mi14020494. Micromachines (Basel). 2023. PMID: 36838194 Free PMC article.
-
Optical spin and orbital Hall effects at the tight focus of the superposition of two coaxial cylindrical vector beams with different-parity numbers.J Opt Soc Am A Opt Image Sci Vis. 2024 Aug 1;41(8):1563-1572. doi: 10.1364/JOSAA.532125. J Opt Soc Am A Opt Image Sci Vis. 2024. PMID: 39873582
-
Spin-Orbital Conversion with the Tight Focus of an Axial Superposition of a High-Order Cylindrical Vector Beam and a Beam with Linear Polarization.Micromachines (Basel). 2022 Jul 15;13(7):1112. doi: 10.3390/mi13071112. Micromachines (Basel). 2022. PMID: 35888930 Free PMC article.
-
Extreme Concentration and Nanoscale Interaction of Light.ACS Photonics. 2022 Jun 15;9(6):1842-1851. doi: 10.1021/acsphotonics.2c00187. Epub 2022 May 24. ACS Photonics. 2022. PMID: 35726245 Free PMC article. Review.
References
-
- Leyder C., Romanelli M., Karr J.P., Giacobino E., Liew T.C.H., Glazov M.M., Kavokin A.V., Malpuech G., Bramati A. Observation of the optical spin Hall effect. Nat. Phys. 2007;3:628–631. doi: 10.1038/nphys676. - DOI
-
- Zhang J., Zhou X.X., Ling X.H., Chen S.Z., Luo H.L., Wen S.C. Orbit-orbit interaction and photonic orbital Hall effect in reflection of a light beam. Chin. Phys. B. 2014;23:064215. doi: 10.1088/1674-1056/23/6/064215. - DOI
Grants and funding
LinkOut - more resources
Full Text Sources

