Predictive coding networks for temporal prediction

Abstract

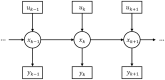
One of the key problems the brain faces is inferring the state of the world from a sequence of dynamically changing stimuli, and it is not yet clear how the sensory system achieves this task. A well-established computational framework for describing perceptual processes in the brain is provided by the theory of predictive coding. Although the original proposals of predictive coding have discussed temporal prediction, later work developing this theory mostly focused on static stimuli, and key questions on neural implementation and computational properties of temporal predictive coding networks remain open. Here, we address these questions and present a formulation of the temporal predictive coding model that can be naturally implemented in recurrent networks, in which activity dynamics rely only on local inputs to the neurons, and learning only utilises local Hebbian plasticity. Additionally, we show that temporal predictive coding networks can approximate the performance of the Kalman filter in predicting behaviour of linear systems, and behave as a variant of a Kalman filter which does not track its own subjective posterior variance. Importantly, temporal predictive coding networks can achieve similar accuracy as the Kalman filter without performing complex mathematical operations, but just employing simple computations that can be implemented by biological networks. Moreover, when trained with natural dynamic inputs, we found that temporal predictive coding can produce Gabor-like, motion-sensitive receptive fields resembling those observed in real neurons in visual areas. In addition, we demonstrate how the model can be effectively generalized to nonlinear systems. Overall, models presented in this paper show how biologically plausible circuits can predict future stimuli and may guide research on understanding specific neural circuits in brain areas involved in temporal prediction.

Fig 1. Graphical model of the generative process assumed by temporal predictive coding.

x_k correspond to hidden states, y_k to observations, and u_k to control inputs. Circles denote latent variables, squares denote observations, and arrows denote conditional dependence of the variables (the absence of an arrow indicates conditional independence).

Fig 2. Possible neural implementations of temporal predictive coding.

A: Potential neural circuit implementing the iterative recurrent predictive coding algorithm. For simplicity, we have depicted each neural ‘layer’ as possessing only two neurons. B: Version of the model where the prediction errors are represented by the difference in membrane potential in soma and at apical dendrites (depicted as ellipses). C: Neural circuitry required to implement the single-iteration predictive coding algorithms. This model no longer includes a separate set of neurons explicitly storing the estimate of the previous timestep, but instead, the temporal prediction errors are computed naturally through recurrent connections. For simplicity, we omitted the control inputs Bu_k, which can be implemented in a similar way to the recurrent inputs $A{\widehat{x}}_{k-1}$ to the error neurons or apical dendrites.

Fig 3. The tracking task and the impact of inference step size and the number of inference steps on performance.

A. The dynamics of the true hidden state are represented as a 3-dimensional vector at each time step, with entries corresponding to position (x₁), velocity (x₂) and acceleration (x₃). B. The projected noisy observations from the true system state in A. C: Estimates of the acceleration with different models, zoomed in at the interval between 560 and 600 time steps. D: MSE difference between tPC and Kalman filter, with varying numbers of inference steps and step sizes for predictive coding. PC stands for temporal predictive coding and KF stands for Kalman filter. All values are with arbitrary units (a.u.).

Fig 4. Effects of learning parameters A and C.

A, B: Estimation of the state and observation trajectories respectively by different models. ‘True’, ‘Learnt’ and ‘Random’ denote the predictive coding model with true, learnt and random A and C respectively. Only the first dimension of the latent and observation is shown for simplicity. The other two dimensions have similar performance. C, D: MSE of the predictions on the hidden and observation levels respectively. Boxplots were obtained with 40 trials for each model. Both x and y are with arbitrary units (a.u.).

Fig 5. Performance with non-identity noise covariance.

A: True and learnt A and C matrices with different underlying noise covariance matrices. B, C: MSE of the predictions on the hidden and observation levels with different noise covariance matrices. Error bars obtained with 40 trials.

Fig 6. Representations developed by the model when trained with patches from movies of dynamic natural scenes.

A: First 10 frames of 2 example training movies used in our experiments. Patches extracted from movies obtained at websites pexels.com, pixabay.com and commons.wikimedia.org (for wikimedia attributions see https://github.com/C16Mftang/temporal-predictive-coding). B: The projective fields C developed Gabor-like filters after training. C: Space-time receptive fields developed by hidden neurons of the tPC model.

Fig 7. Simulations of the pendulum.

A: A free-body diagram of a simple pendulum that has a mass m attached to a string with length L. Also shown are the forces applied to the mass. The restoring force −mg sin θ is a net force toward the equilibrium position. B: A phase portrait of the pendulum simulation showing the result of our linear versus nonlinear models prediction for the ground-truth data. The vector field (i.e. set of small arrows) was created by computing the derivatives of $\frac{d{\theta }_1}{dt}$ and $\frac{d{\theta }_2}{dt}$ at t = 0 on a grid of 30 points over the range of −π to + π and -4 to +4 for θ₁ and θ₂, respectively. C: The barplot shows the difference between the mean prediction errors of the linear model versus the nonlinear model from 100 simulations with varying noise profiles. The mean errors are significantly different (p << 0.001).