Scattering spectra models for physics

Abstract

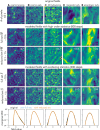
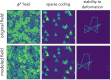
Physicists routinely need probabilistic models for a number of tasks such as parameter inference or the generation of new realizations of a field. Establishing such models for highly non-Gaussian fields is a challenge, especially when the number of samples is limited. In this paper, we introduce scattering spectra models for stationary fields and we show that they provide accurate and robust statistical descriptions of a wide range of fields encountered in physics. These models are based on covariances of scattering coefficients, i.e. wavelet decomposition of a field coupled with a pointwise modulus. After introducing useful dimension reductions taking advantage of the regularity of a field under rotation and scaling, we validate these models on various multiscale physical fields and demonstrate that they reproduce standard statistics, including spatial moments up to fourth order. The scattering spectra provide us with a low-dimensional structured representation that captures key properties encountered in a wide range of physical fields. These generic models can be used for data exploration, classification, parameter inference, symmetry detection, and component separation.

Keywords: Gibbs energy; reduced models; wavelets.

Fig. 1.

Steps to build a feasible model for a random field x from only one or a few realizations. We first build a low-dimensional representation $\mathrm{\Phi }(x)$ of the random field, which specifies a maximum entropy model. The representation $\mathrm{\Phi }(x)$ is obtained by conducting the wavelet transform Wx and its modulus $|Wx|$, and then computing the means and covariance of all wavelet channels $(Wx,|Wx|)$. Such a covariance matrix is further binned and sampled using wavelets to reduce its dimensionality, which is called the scattering spectra $\overline{S}(x)$. Finally, These scattering spectra are renormalized and reduced in dimension by thresholding its Fourier coefficients along rotation and scale parameters $\mathrm{\Phi }(x)=P\overline{S}$, making use of the regularity properties of the field. For many physical fields, this representation can be as small as only around $\sim {10}^2$ coefficients for a 256×256 field.

Fig. 2.

a) For $\lambda \ne {\lambda }^{\prime }$, the Fourier supports of $x\star {\psi }_{\lambda }$ and $x\star {\psi }_{{\lambda }^{\prime }}$ typically do not overlap. b) The Fourier support of $|x\star {\psi }_{\lambda }{|}^2$ is twice larger and centered at 0 and hence overlaps with $x\star {\psi }_{{\lambda }^{\prime }}$ if $|{\lambda }^{\prime }|\le |\lambda |$. c) The Fourier support of $|x\star {\psi }_{\lambda }|$ is also centered at 0 and hence overlaps with $x\star {\psi }_{{\lambda }^{\prime }}$ if $|{\lambda }^{\prime }|<|\lambda |$.

Fig. 3.

Visual comparison of realistic physical fields and those sampled from maximum entropy models based on wavelet higher order moments $\overline{M}$ and wavelet scattering spectra $\overline{S}$ statistics. The first row shows five example fields from physical simulations of cosmic lensing, cosmic web, 2D turbulence, magnetic turbulence, and squeezed turbulence. The second and third rows show syntheses based on the selected high-order wavelet statistics estimated from 100 realizations. They are obtained from a microcanonical sampling with 800 steps. The fourth and fifth rows show similar syntheses based on the scattering spectra statistics, with only 200 steps of the sampling run. This figure shows visually that the scattering spectra can model well the statistical properties of morphology in many physical fields, while the high-order statistics either fail to do so or converge at a much slower rate. To clearly show the morphology of structures at small scales, we show a zoom-in of $128\times 128$ pixels regions. Finally, to quantitatively validate the goodness of the scattering model, we show the marginal PDF (histogram) comparison in the last row.

Fig. 4.

Validation of the scattering maximum entropy models for the five physical fields A–E by various test statistics. The curves for field E represent the original statistics and those for A–D are shifted upwards by an offset. In general, our scattering spectra models well reproduce the validation statistics of the five physical fields.

Fig. 5.

Visual interpretation of the scattering spectra. The central field is one realization of field B in physical simulations. The other four panels are generated fields with two simple collective modifications of the scattering spectra coefficients.

Fig. 6.

Example of failures and applications beyond typical physical fields. The modeled field of the central panel has been recentered for easier comparison with the original ones.