Linking fast and slow: The case for generative models
- PMID: 38562283
- PMCID: PMC10861163
- DOI: 10.1162/netn_a_00343
Linking fast and slow: The case for generative models
Abstract
A pervasive challenge in neuroscience is testing whether neuronal connectivity changes over time due to specific causes, such as stimuli, events, or clinical interventions. Recent hardware innovations and falling data storage costs enable longer, more naturalistic neuronal recordings. The implicit opportunity for understanding the self-organised brain calls for new analysis methods that link temporal scales: from the order of milliseconds over which neuronal dynamics evolve, to the order of minutes, days, or even years over which experimental observations unfold. This review article demonstrates how hierarchical generative models and Bayesian inference help to characterise neuronal activity across different time scales. Crucially, these methods go beyond describing statistical associations among observations and enable inference about underlying mechanisms. We offer an overview of fundamental concepts in state-space modeling and suggest a taxonomy for these methods. Additionally, we introduce key mathematical principles that underscore a separation of temporal scales, such as the slaving principle, and review Bayesian methods that are being used to test hypotheses about the brain with multiscale data. We hope that this review will serve as a useful primer for experimental and computational neuroscientists on the state of the art and current directions of travel in the complex systems modelling literature.
Keywords: Bayesian statistics; Dynamical systems; Generative models; Hidden Markov models; Hierarchical modelling; Temporal scales.
© 2023 Massachusetts Institute of Technology.
Conflict of interest statement
Competing Interests: The authors have declared that no competing interests exist.
Figures
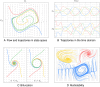
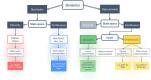
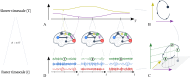

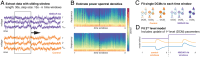
Similar articles
-
Neuronal Sequence Models for Bayesian Online Inference.Front Artif Intell. 2021 May 21;4:530937. doi: 10.3389/frai.2021.530937. eCollection 2021. Front Artif Intell. 2021. PMID: 34095815 Free PMC article. Review.
-
Likelihood approximation networks (LANs) for fast inference of simulation models in cognitive neuroscience.Elife. 2021 Apr 6;10:e65074. doi: 10.7554/eLife.65074. Elife. 2021. PMID: 33821788 Free PMC article.
-
Modeling and inference methods for switching regime-dependent dynamical systems with multiscale neural observations.J Neural Eng. 2022 Nov 28;19(6). doi: 10.1088/1741-2552/ac9b94. J Neural Eng. 2022. PMID: 36261030
-
[Dynamic paradigm in psychopathology: "chaos theory", from physics to psychiatry].Encephale. 2001 May-Jun;27(3):260-8. Encephale. 2001. PMID: 11488256 French.
-
Analyzing the brain's dynamic response to targeted stimulation using generative modeling.Netw Neurosci. 2025 Mar 5;9(1):237-258. doi: 10.1162/netn_a_00433. eCollection 2025. Netw Neurosci. 2025. PMID: 40161996 Free PMC article. Review.
Cited by
-
A Broken Duet: Multistable Dynamics in Dyadic Interactions.Entropy (Basel). 2024 Aug 28;26(9):731. doi: 10.3390/e26090731. Entropy (Basel). 2024. PMID: 39330066 Free PMC article.
-
BSD: A Bayesian Framework for Parametric Models of Neural Spectra.Eur J Neurosci. 2025 May;61(10):e70149. doi: 10.1111/ejn.70149. Eur J Neurosci. 2025. PMID: 40415547 Free PMC article.
-
Assessing time series correlation significance: A parametric approach with application to physiological signals.Biomed Signal Process Control. 2024 Aug;94:106235. doi: 10.1016/j.bspc.2024.106235. Biomed Signal Process Control. 2024. PMID: 39846001 Free PMC article.
References
-
- Arnold, L. (1995). Random dynamical systems. Berlin: Springer. 10.1007/BFb0095238 - DOI
-
- Beal, M. J., & Ghahramani, Z. (2003). The variational Bayesian EM algorithm for incomplete data: With application to scoring graphical model structures. In Lindley V. and others (Eds.), Bayesian Statistics 7: Proceedings of the Seventh Valencia International Meeting (pp. 453–463). 10.1093/oso/9780198526155.003.0025 - DOI
Publication types
LinkOut - more resources
Full Text Sources
