The Demographic-Wealth model for cliodynamics

Abstract

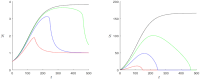
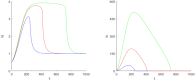
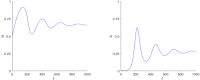
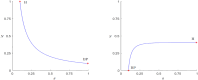
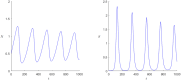
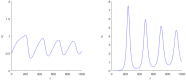
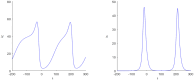
Cliodynamics is a still a relatively new research area with the purpose of investigating and modelling historical processes. One of its first important mathematical models was proposed by Turchin and called "Demographic-Fiscal Model" (DFM). This DFM was one of the first and is one of a few models that link population with state dynamics. In this work, we propose a possible alternative to the classical Turchin DFM, which contributes to further model development and comparison essential for the field of cliodynamics. Our "Demographic-Wealth Model" (DWM) aims to also model link between population and state dynamics but makes different modelling assumptions, particularly about the type of possible taxation. As an important contribution, we employ tools from nonlinear dynamics, e.g., existence theory for periodic orbits as well as analytical and numerical bifurcation analysis, to analyze the DWM. We believe that these tools can also be helpful for many other current and future models in cliodynamics. One particular focus of our analysis is the occurrence of Hopf bifurcations. Therefore, a detailed analysis is developed regarding equilibria and their possible bifurcations. Especially noticeable is the behavior of the so-called coexistence point. While changing different parameters, a variety of Hopf bifurcations occur. In addition, it is indicated, what role Hopf bifurcations may play in the interplay between population and state dynamics. There are critical values of different parameters that yield periodic behavior and limit cycles when exceeded, similar to the "paradox of enrichment" known in ecology. This means that the DWM provides one possible avenue setup to explain in a simple format the existence of secular cycles, which have been observed in historical data. In summary, our model aims to balance simplicity, linking to the underlying processes and the goal to represent secular cycles.

Fig 1. Dynamics of model (1).

Initial Values: N₀ = 0.5, S₀ = 0. Parameters: k₀ = 1, r = 0.02, ρ₀ = 1, c = 3, s₀ = 10. Values for β: red ≡ 0.4, blue ≡ 0.25, green ≡ 0.1, black ≡ 0.

Fig 2. Dynamics of model (1).

Initial Values: N₀ = 0.5, S₀ = 0. Parameters: k₀ = 1, r = 0.02, β = 0.25, c = 3, s₀ = 10. Values for ρ₀: blue ≡ 1, red ≡ 2, green ≡ 4.

Fig 3. Dynamics of the “Demographic-Wealth model” with stable equilibrium (N*, S*).

Parameters: r = 0.02, g = 0.15, a = 0.05, b = 0.1, c = 0.5, k₀ = 1, d = 1. Initial values: N₀ = 0.5, S₀ = 0.01.

Fig 4. Equilibrium point continuation for the parameter g.

Existence of a Branch point at g = 0.1 where the equilibrium (N*, S*) becomes stable. Supercritical Hopf bifurcation at g = 0.992, 1st Lyapunov coefficient <0.

Fig 5. Equilibrium point continuation for the parameter β.

Existence of a Branch point at β = 0.15 where the equilibrium (N*, S*) looses its stability. Supercritical Hopf bifurcation at β = 0.015, 1st Lyapunov coefficient <0.

Fig 6. Equilibrium point continuation for the parameter k₀.

Branch point at $k_0=\frac{2}{3}$ where the equilibrium (N*, S*) becomes stable. Supercritical Hopf bifurcation at k₀ = 2.095, 1st Lyapunov coefficient < 0.

Fig 7. Periodic orbit continuation for the parameter k₀.

Continuation of the Hopf bifurcation at k₀ = 2.095, as in Fig 6. The amplitude of the periodic orbit is growing upon increasing the carrying capacity and it eventually comes close to zero population level. In particular, we have the hallmarks of the paradox of enrichment.

Fig 8. Dynamics of the Demographic-Wealth model with stable equilibrium (N*, S*).

Parameters: r = 0.02, g = 0.15, a = 0.05, b = 0.1, c = 0.5, k₀ = 2, d = 1. Initial values: N₀ = 0.5, S₀ = 0.01.

Fig 9. Dynamics of the Demographic-Wealth model with stable equilibrium (N*, S*).

Parameters: r = 0.1, g = 0.15, a = 0.05, b = 0.1, c = 0.5, k₀ = 1, d = 1. Initial values: N₀ = 0.5, S₀ = 0.01.

Fig 10. Dynamics of the Demographic-Wealth model with stable equilibrium (N*, S*).

Parameters: r = 0.02, g = 0.15, a = 0.01, b = 0.1, c = 0.5, k₀ = 1, d = 1. Initial values: N₀ = 0.5, S₀ = 0.01.

Fig 11. Dynamics of the Demographic-Wealth model with limit cycle and adapted axes.

Parameters: r = 0.04, g = 0.16, a = 0.006, b = 0.1, c = 0.5, k₀ = 1, d = 1. Initial values: N₀ = 0.33, S₀ = 0.01.