Efficient telecom-to-visible spectral translation through ultra-low power nonlinear nanophotonics

Abstract

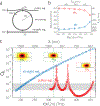
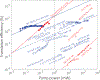
The ability to spectrally translate lightwave signals in a compact, low-power platform is at the heart of the promise of nonlinear nanophotonic technologies. For example, a device to link the telecommunications band with visible and short near-infrared wavelengths can enable a connection between high-performance chip-integrated lasers based on scalable nanofabrication technology with atomic systems used for time and frequency metrology. While second-order nonlinear (${\chi }^{\left(2\right)}$) systems are the natural approach for bridging such large spectral gaps, here we show that third-order nonlinear (${\chi }^{\left(3\right)}$) systems, despite their typically much weaker nonlinear response, can realize spectral translation with unprecedented performance. By combining resonant enhancement with nanophotonic mode engineering in a silicon nitride microring resonator, we demonstrate efficient spectral translation of a continuous-wave signal from the telecom band (≈ 1550 nm) to the visible band (≈ 650 nm) through cavity-enhanced four-wave mixing. We achieve such translation over a wide spectral range >250 THz with a translation efficiency of (30.1 ± 2.8) % and using an ultra-low pump power of (329 ± 13) μW. The translation efficiency projects to (274 ± 28) % at 1 mW and is more than an order of magnitude larger than what has been achieved in current nanophotonic devices.

FIG. 1:. Nanophotonic telecom-to-visible spectral translation and efficiency comparison.

a, Nanophotonic spectral translation uses a cavity-enhanced second-order or third-order nonlinear optical process (${\chi }^{(2)}$ or ${\chi }^{(3)}$) to efficiently transfer light into a new frequency with ultra-low laser pump power (see inset for a simplified scheme). ${\omega }_p$, ${\omega }_t$, and ${\omega }_v$ represent frequencies for pump, telecom, and visible light, respectively. b, Energy and momentum conservation requirements for sum-frequency generation (SFG, left) and degenerate four-wave mixing (dFWM, right) processes with single fundamental mode family (SFMF) operation. c, False-colored scanning-electron-microscope image of the nanophotonic device and the coupling scheme we use for spectral translation. The top pulley waveguide (red) and the bottom straight waveguide (blue) are used to couple pump/visible and telecom light, respectively, into and out of the microring (green). d, Order-of-magnitude comparison of the translation efficiency for the two processes in (b) with the device geometry of (c). For a microring with a finesse of $𝓕\approx 5000$ (red), the efficiency of the ${\chi }^{(3)}$ process can compete with, or even exceed, that of the ${\chi }^{(2)}$ process at mW-pumping levels, if the mode overlap can be sufficiently well-optimized. See Supplementary Information for details.

FIG. 2:. Design for telecom-to-visible spectral translation.

a, Device scheme. $RR/RW$: ring outer radius/ring width. $PW/PG$: pulley waveguide width/gap. $SW/SG$: straight waveguide width/gap. wg: waveguide. b, Simulations of the frequency/phase-matched wavelengths. The $m$ numbers of the three modes satisfy $\left(2m_{\text{p}}=m_{\text{t}}+m_{\text{v}}\right)$, with a frequency mismatch $\text{Δ}\omega /(2\pi )=\left|2{\omega }_{\text{p}}-{\omega }_{\text{t}}-{\omega }_{\text{v}}\right|/(2\pi )$ within 1 GHz. Simulation parameters are $H=500\text{nm}$, $RR=25\mu \text{m}$, and $RW=1158\text{nm}$. c, Wavelength-dependent coupling of the pulley (red) and straight (blue) waveguides. Targeted values are typically $Q_{\text{c}}={10}^5$ to 10⁶ (gray area). All modes are fundamental transverse electric modes (TE1), with a cross-section view of the dominant electric field amplitude (in the radial direction of the microring) shown in the insets. Simulation parameters (in addition to b): $PW=560\text{nm}$, $PG=170\text{nm}$, $SW=1120\text{nm}$, and $SG=425\text{nm}$.

FIG. 3:. Assessment of device Q, coupling, and phase- and frequency-matching.

a, Cavity transmission for the spectral translation device in visible, pump, and telecom bands, with device parameters prescribed in Fig. 2(c). b, Zoom-in transmission traces for TE1 modes at 665.8 nm (red), 939.5 nm (green), and 1572.7 nm (blue) from left to right with loaded $Q$ factors of ≈ (1 – 3) × 10⁵ estimated by Lorentzian fitting (red lines). c-d, Visible-telecom photon-pair spectra by spontaneous four-wave mixing, with a degenerate pump at 939.5 nm. Inset of ¸ shows the visible spectrum in log scale. The 669.8 nm/1572.7 nm photon-pair spectra are free from broadband noise and are > 16 dB larger than adjacent mode sets, which indicates good frequency- and phase-matching for the dFWM process.

FIG. 4:. Telecom-to-visible nanophotonic spectral translation.

a, Optical spectra recorded in the pulley (red) and straight (blue) waveguides for the spectral translation device. The telecom light at 1572.7 nm (blue) is transferred to a visible wavelength at 669.8 nm (red) through a pump at 939.5 nm, with no other translation channels or noise contribution observed. 0 dB is referenced to 1 mW (i.e., dBm). b, A dichroic filter is used to reject the pump light (> 80 dB) in order to calibrate the visible power accurately in pump-power dependent measurements. c, Translation efficiency ($\eta$, left y-axis) and quantum efficiency (${\eta }_{\text{Q}}$, right y-axis) versus pump power. A translation efficiency $\eta =(30.1\pm 2.8)\text{\%}$ is achieved for (329 ± 13) μW pump power. The quadratic dependence on pump power is a signature of the degenerate four-wave mixing process. Solid and dashed red lines represent the quadratic fitting and its one standard deviation confidence range. Insets show the corresponding pump transmission traces. The pump detuning is brought close to the bottom of the transmission dip to maximize the translation efficiency. d, Output visible power as a function of input telecom power for a fixed pump power of (165 ± 7) μW, with a translation efficiency determined by a linear fit of $\eta =(7.5\pm 0.4)\text{\%}$. The pump detuning is kept constant as indicated by the open circle in the inset transmission trace. Solid and dashed red lines represent the linear fitting and its one standard deviation confidence range. Error bars in c-d are one standard deviation uncertainties originating from calibration of the on-chip power.

FIG. 5:. Comparison of our nanophotonic spectral translation efficiency with state-of-the-art results.

We compare our results with other state-of-the-art devices in terms of translation efficiency vs. pump power. Solid/dashed lines show the scaling in ${\chi }^{(2)}$ LiNbO₃ (blue) and ${\chi }^{(3)}$ Si₃N₄ (red) resonators/waveguides, respectively, which agree with theoretical estimates in that ${\chi }^{(2)}$ and ${\chi }^{(3)}$ processes have linear and quadratic power scaling, respectively (Ref. is distinguished from others due to its cavity frequency mismatch.). Through resonance enhancement and careful mode engineering, our ${\chi }^{(3)}$ device is projected to reach a translation efficiency of (274 ± 28) % at 1 mW, which is comparable to that of the best ${\chi }^{(2)}$ device. This represents a many order of magnitude improvement relative to the waveguide case, where the ${\chi }^{(3)}$ process is over 50 dB smaller in efficiency than the ${\chi }^{(2)}$ case at 10 mW, μ: micro. wg: waveguide.