Approaching the Complete Basis Set Limit for Spin-State Energetics of Mononuclear First-Row Transition Metal Complexes
- PMID: 38574194
- PMCID: PMC11044276
- DOI: 10.1021/acs.jctc.4c00092
Approaching the Complete Basis Set Limit for Spin-State Energetics of Mononuclear First-Row Transition Metal Complexes
Abstract
Convergence to the complete basis set (CBS) limit is analyzed for the problem of spin-state energetics in mononuclear first-row transition metal (TM) complexes by taking under scrutiny a benchmark set of 18 energy differences between spin states for 13 chemically diverse TM complexes. The performance of conventional CCSD(T) and explicitly correlated CCSD(T)-F12a/b calculations in approaching the CCSD(T)/CBS limits is systematically studied. An economic computational protocol is developed based on the CCSD-F12a approximation and (here proposed) modified scaling of the perturbative triples term (T#). This computational protocol recovers the relative spin-state energetics of the benchmark set in excellent agreement with the reference CCSD(T)/CBS limits (mean absolute deviation of 0.4, mean signed deviation of 0.2, and maximum deviation of 0.8 kcal/mol) and enables performing canonical CCSD(T) calculations for mononuclear TM complexes sized up to ca. 50 atoms, which is illustrated by application to heme-related metalloporphyrins. Furthermore, a good transferability of the basis set incompleteness error (BSIE) is demonstrated for spin-state energetics computed using CCSD(T) and other wave function methods (MP2, CASPT2, CASPT2/CC, NEVPT2, and MRCI + Q), which justifies efficient focal-point approximations and simplifies the construction of multimethod benchmark studies.
Conflict of interest statement
The authors declare no competing financial interest.
Figures

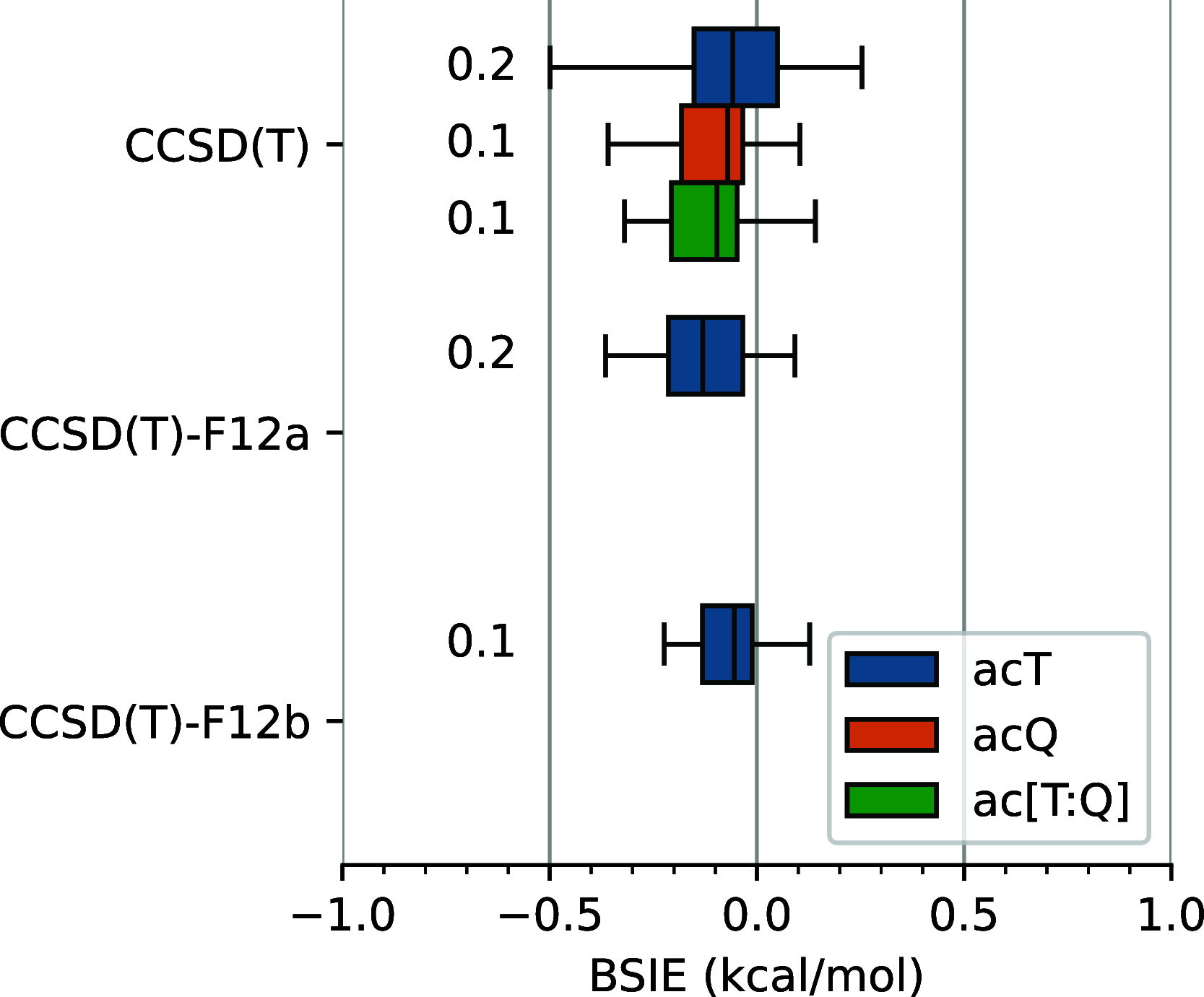
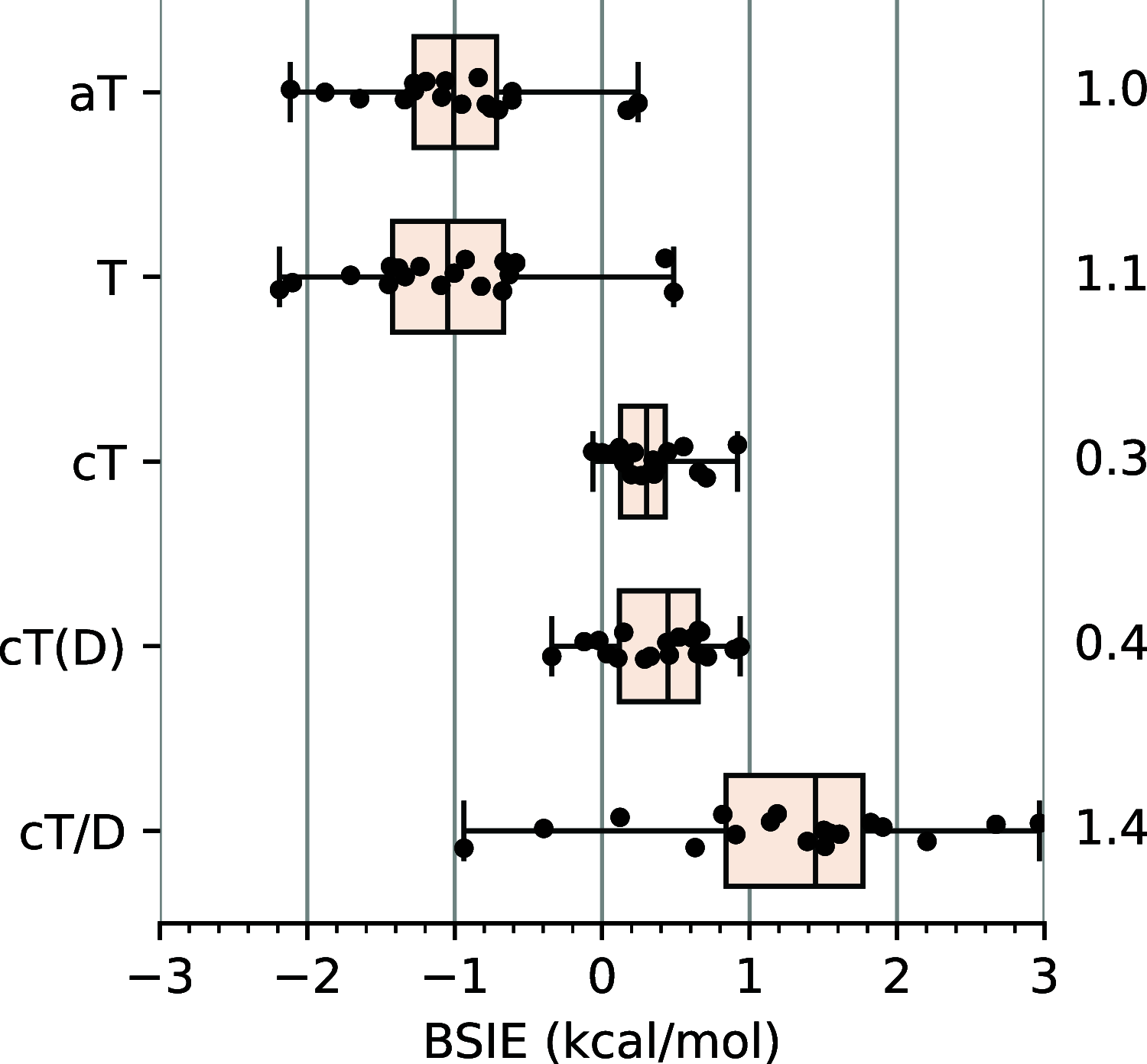

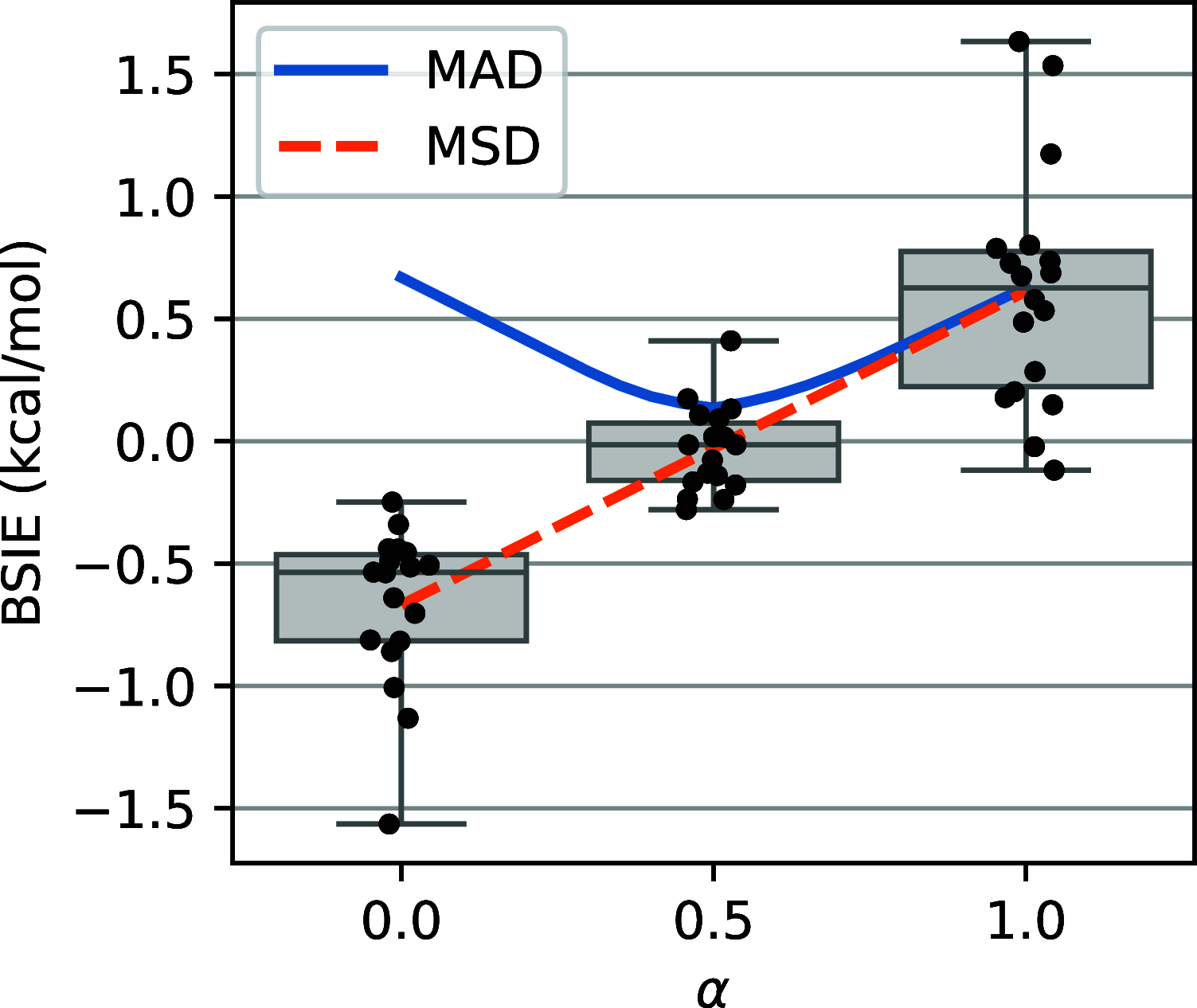
 corresponding to the (T#) correction proposed
in this work. For numerical data of individual complexes, see
corresponding to the (T#) correction proposed
in this work. For numerical data of individual complexes, see 
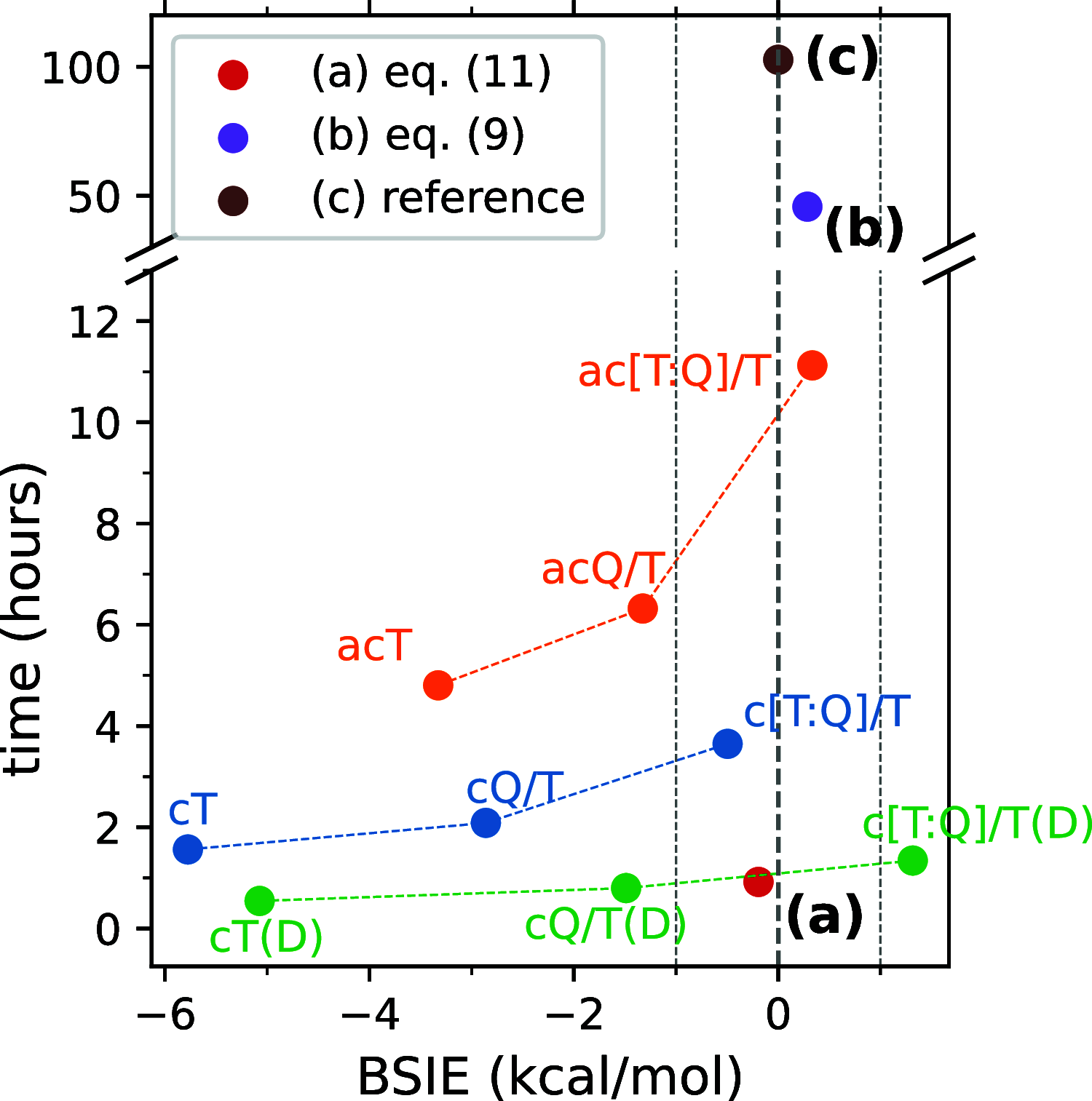
 at the CCSD(T) level: (a) the CCSD(T#)-F12a/cT(D)
protocol of eq 11 (b) the CCSD(T)-F12b/a[T:Q]
+ Δ3s3p-F12b/acT protocol of eq 9 and
(c) the reference CBS extrapolation ac[Q:5]/Q, and some other conventional
CCSD(T) calculations and extrapolations (see Section 2.4 for the notation of basis sets and extrapolations).
The reported times are obtained by summing the wall clock times needed
to compute the energies of the two spin states. All times were measured
using Molpro 2019.2 running 12 MPI processes, each allocating up to
24 GB of RAM, on an Intel Xeon 6146 system equipped with triple RAID-0
of Intel P4600 solid-state drives.
at the CCSD(T) level: (a) the CCSD(T#)-F12a/cT(D)
protocol of eq 11 (b) the CCSD(T)-F12b/a[T:Q]
+ Δ3s3p-F12b/acT protocol of eq 9 and
(c) the reference CBS extrapolation ac[Q:5]/Q, and some other conventional
CCSD(T) calculations and extrapolations (see Section 2.4 for the notation of basis sets and extrapolations).
The reported times are obtained by summing the wall clock times needed
to compute the energies of the two spin states. All times were measured
using Molpro 2019.2 running 12 MPI processes, each allocating up to
24 GB of RAM, on an Intel Xeon 6146 system equipped with triple RAID-0
of Intel P4600 solid-state drives.



 .
.Similar articles
-
Performance of quantum chemistry methods for a benchmark set of spin-state energetics derived from experimental data of 17 transition metal complexes (SSE17).Chem Sci. 2024 Oct 28;15(48):20189-20204. doi: 10.1039/d4sc05471g. eCollection 2024 Dec 11. Chem Sci. 2024. PMID: 39574537 Free PMC article.
-
The curious case of DMSO: A CCSD(T)/CBS(aQ56+d) benchmark and DFT study.J Chem Phys. 2021 Sep 21;155(11):114304. doi: 10.1063/5.0057327. J Chem Phys. 2021. PMID: 34551533
-
Benchmark theoretical study of the π-π binding energy in the benzene dimer.J Phys Chem A. 2014 Sep 4;118(35):7568-78. doi: 10.1021/jp5024235. Epub 2014 May 5. J Phys Chem A. 2014. PMID: 24761749
-
Extrapolating MP2 and CCSD explicitly correlated correlation energies to the complete basis set limit with first and second row correlation consistent basis sets.J Chem Phys. 2009 Nov 21;131(19):194105. doi: 10.1063/1.3265857. J Chem Phys. 2009. PMID: 19929044
-
Calculations on noncovalent interactions and databases of benchmark interaction energies.Acc Chem Res. 2012 Apr 17;45(4):663-72. doi: 10.1021/ar200255p. Epub 2012 Jan 6. Acc Chem Res. 2012. PMID: 22225511 Review.
Cited by
-
Rationalizing Spin-Crossover Properties of Substituted Fe (II) Complexes.Inorg Chem. 2025 Aug 4;64(30):15437-15447. doi: 10.1021/acs.inorgchem.5c01523. Epub 2025 Jul 23. Inorg Chem. 2025. PMID: 40699315 Free PMC article.
-
Performance of quantum chemistry methods for a benchmark set of spin-state energetics derived from experimental data of 17 transition metal complexes (SSE17).Chem Sci. 2024 Oct 28;15(48):20189-20204. doi: 10.1039/d4sc05471g. eCollection 2024 Dec 11. Chem Sci. 2024. PMID: 39574537 Free PMC article.
References
-
- Swart M., Costas M., Eds. In Spin States in Bioinorganic and Inorganic Chemistry: Influence on Structure and Reactivity; Wiley, 2015.
-
- Swart M.New Directions in the Modeling of Organometallic Reactions. In Topics in Organometallic Chemistry; Springer: Cham, 2020; Vol. 67, pp 191–226.
-
- Kepp K. P. In Transition Metals in Coordination Environments: Computational Chemistry and Catalysis Viewpoints; Broclawik E., Borowski T., Radoń M., Eds.; Challenges and Advances in Computational Chemistry and Physics; Springer International Publishing: Cham, 2019; Vol. 29, Chapter 1, pp 1–33.
-
- Harvey J. N. On the accuracy of density functional theory in transition metal chemistry. Annu. Rep. Prog. Chem., Sect. C: Phys. Chem. 2006, 102, 203–226. 10.1039/b419105f. - DOI
LinkOut - more resources
Full Text Sources
