Integrated mechanical computing for autonomous soft machines

Abstract

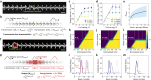
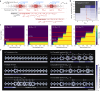
Mechanical computing offers a new modality to formulate computational autonomy in intelligent matter or machines without any external powering or active elements. Transition (or solitary) waves, induced by nonreciprocity in mechanical metamaterials comprising a chain of bistable elements, have proven to be a key ingredient for dissipation-free transmission and computation of mechanical information. However, advanced processing of mechanical information in existing designs is hindered by its dissipation when interacting with networked logic gates. Here, we present a metamaterial design strategy that allows non-dispersive mechanical solitary waves to compute multi-level cascaded logic functions, termed 'integrated mechanical computing', by propagating through a network of structurally heterogeneous computing units. From a perspective of characteristic potential energy, we establish an analytical framework that helps in understanding the solitary wave-based mechanical computation, and governs the mechanical design of key determinants for realizing cascaded logic computation, such as soliton profile and logic elements. The developed integrated mechanical computing systems are shown to receive, transmit and compute mechanical information to actuate intelligent soft machine prototypes in a seamless and integrated manner. These findings would pave the way for future intelligent robots and machines that perform computational operations between various non-electrical environmental inputs.

Fig. 1. Design concept of integrated mechanical computing.

a Unit cells, their topological assembly for computational logics, and system architectures for integrated mechanical computing. b Schematic of a unit bistable element with programmable characteristic energy components: the input energy barrier, $U_b^1$, and the output transmissive energy, $U_{out}^1$. c A set of schematics describing solitary wave-based mechanical computing processes: solitary information that propagates through mechanical transmission lines with (i) the input energy barrier, $U_b^T$, and the output transmissive energy, $U_{out}^T$, satisfying $U_b^T<U_{out}^T$, (ii) a mechanologic having small $U_b^{X_s}$ such that $U_{out}^T>U_b^{X_s+T}$, which permits computational propagation, (iii) a mechanologic having large $U_b^{X_l}$ such that $U_{out}^T<U_b^{X_l+T}$, which leads to the transmission failure, that is, information dissipation, (iv) a cascade of mechanologics characterized by accumulated mechanical impedance that increases the input energy barrier for computation, and (v) our design approach featuring a cascade of rationally designed mechanologics to alleviate the coupled U_b issue. d Qualitative U_b profiles as a function of position for the solitary wave propagations shown in c.

Fig. 2. Design and characterization of solitary wave-based computational propagation.

a Typical propagation behavior of mechanical solitary information through a mechanical transmission line (Supplementary Movie 1). Scale bar, 1 cm. b Schematic diagram of the mechanical transmission line consisting of N ( = N₁ + N₂) elements with input, $U_b^T$, and output, $U_{out}^T$ characteristic energy components (see Methods). c, d Experimentally obtained $U_b^T$ and $U_{out}^T$ of transmission lines with N varying from 0 to 9. e Numerically estimated N_soliton as a function of the normalized spring stiffness (k/k₀) with k₀ = 180 N m^-1. f Typical propagation behavior of mechanical solitary information through a transmission line that contains a structurally heterogeneous computing unit (Supplementary Movie 1). Scale bar, 1 cm. g, Schematic diagram of the transmission line connected with a mechanical computing unit X (see Methods). h, j, l Numerical studies on the evolution of the normalized displacement of each bistable unit in homogeneous transmission (mechanical impedance, R₀) (h) and computational transmission through a computing unit having a mechanical impedance (R) of 10R₀ (j) and 20R₀ (l) (Supplementary Movie 2). The variable mechanical impedance is defined only for the tenth spring. A color bar indicates normalized displacement. i, k, m The time-evolving propagation behav_ior of the instability factor (S_i) along with the system shown in h, j, l, respectively. All error bounds indicate SD.

Fig. 3. Architected design and characterization of mechanologics.

a Design strategy for mechanologics defined within a unit square lattice. b Schematic symbols, architected designs, and photographs of computational mechanologics (NOT, AND, and OR gates). The as-fabricated precursor designs, highlighted in gray, are transformed into the preset buckled states, highlighted in blue, when placed into the lattice frame. See Supplementary Fig. 10 and Methods for the details on the mechanologic design. Scale bar, 1 cm. c Experimental characterization of bistable profiles of the mechanologics with transmission lines (N₂ = 6) connected behind them. d Experimental characterization of effective energy barriers against computational propagation through the mechanologics as a function of the length (characterized by N₂) of the transmission line connected behind it. e Time-evolving normalized displacement data showing the experimental performance of mechanologics (Supplementary Movies 3–5). Detailed beam configurations for the analyses are shown in Supplementary Fig. 10. Color bars indicate normalized displacement. All error bounds indicate SD.

Fig. 4. Computational propagation through one-dimensionally (1D) cascaded mechanologics.

a Schematic description of the general design rule for cascaded computation. b Simulation results of cascaded computations through a 1D network of mechanologics (mechanical impedance, R) connected by transmission lines (mechanical impedance, R₀) with varying N_cas (0 to 5). The normalized time taken to complete the propagation was introduced not only to characterize the propagation performance, but to indirectly estimate the effective mechanical impedance of overall cascaded systems. c Numerical studies on the evolution of the normalized displacement of each bistable unit in computational propagations through cascaded mechanologics (mechanical impedance, R = 15R₀) with N_cas = 0 (i), 1 (ii), 3 (iii), 5 (iv) (Supplementary Movie 6). d Experimental verification of the proposed design rule for cascaded computing (Supplementary Movie 7). To demonstrate 1D cascaded computing, mechanical inverters with two different phases (ϕ = 0, π) were connected in series. The time parameter, which has a linear relationship with mechanical impedance for propagation, was obtained for every bistable beam to characterize the behavior of cascaded computing. Scale bar, 2 cm.

Fig. 5. Computational propagation through two-dimensionally (2D) cascaded mechanologics.

a A logic diagram example for the 2D cascaded computing demonstration. b,d Physical implementation of the 2D integrated mechanical computing circuit shown in (a). The system consists of four mechanologics and six redirector units, networked by transmission lines with N_cas = 0 (b) and N_cas = 2 (d). c, e Operation of the mechanical circuit upon stimulation of mechanical inputs (A₁, B₁) (left) and (A₁, B₁, A₂, B₂) (right) (Supplementary Movie 8). The computing failure for c, highlighted in red, was due to the excessive energy barrier accumulated from cascaded mechanical components. By contrast, the increase in N_cas permitted successful propagation through 3-level cascaded mechanologics (e). All scale bars, 2 cm.

Fig. 6. Autonomous soft machines based on integrated mechanical computing.

a Schematic illustration of the force-dependent thigmonastic movements of M. pudica (Supplementary Movie 9). b Schematic illustration of the design and actuation mechanism of soft hydrogel actuators. c Photographs of the reservoirs mounted monolithically on the transmission line for water droplet transport with a volume up to 30 μL. d Typical actuation behaviors of the hydrogel actuator upon water uptake with volume of 10, 20, and 30 μL, respectively from left to right (Supplementary Movie 10). e A soft machine consisting of ten soft actuators connected in series via the mechanical transmission line (left) and its sequential actuation upon mechanical stimulation (right) (Supplementary Movie 11). f Photograph of the autonomous soft machine that reproduces the function of the internal operating circuit of M. pudica as described in (a). The system consists of double-layered integrated mechanical computing circuits (1 AND gate and 3 OR gates) and 17 soft actuators arranged within two different branches. g, h Operation of the integrated mechano-intelligence (g) and resulting force-dependent actuation sequences (h) (Supplementary Movie 12). Scale bars, 1 cm (c–e) and 2 cm (f).