A computational model of Alzheimer's disease at the nano, micro, and macroscales

Abstract

Introduction: Mathematical models play a crucial role in investigating complex biological systems, enabling a comprehensive understanding of interactions among various components and facilitating in silico testing of intervention strategies. Alzheimer's disease (AD) is characterized by multifactorial causes and intricate interactions among biological entities, necessitating a personalized approach due to the lack of effective treatments. Therefore, mathematical models offer promise as indispensable tools in combating AD. However, existing models in this emerging field often suffer from limitations such as inadequate validation or a narrow focus on single proteins or pathways.

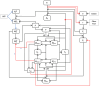
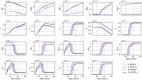
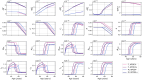
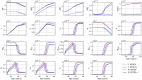
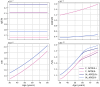
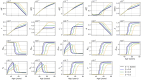
Methods: In this paper, we present a multiscale mathematical model that describes the progression of AD through a system of 19 ordinary differential equations. The equations describe the evolution of proteins (nanoscale), cell populations (microscale), and organ-level structures (macroscale) over a 50-year lifespan, as they relate to amyloid and tau accumulation, inflammation, and neuronal death.

Results: Distinguishing our model is a robust foundation in biological principles, ensuring improved justification for the included equations, and rigorous parameter justification derived from published experimental literature.

Conclusion: This model represents an essential initial step toward constructing a predictive framework, which holds significant potential for identifying effective therapeutic targets in the fight against AD.

Keywords: APOE; Alzheimer's disease; amyloid beta; complex biological systems; mathematical models; ordinary differential equations; personalized approach; tau proteins.

Figure 1

Model schematic. Our hypothesis can be summarized in the model schematic. We propose that the relationships between entities, evolving dynamically through time, is sufficient to explain the decline in neurons, rise of inflammation, and increases in both amyloid plaques and tau tangles that is seen in aging, up to and including Alzheimer's disease, without requiring an external “catalytic” event such as reactive oxygen species production. This is a multi-factorial, multi-parametric viewpoint, quite different from other hypotheses in the literature. Blue arrows and asterisk identify an APOE4-dependent relation. Red arrows identify degradation relations, and red lines ending with a dot is for inhibition.

Figure 2

Concentration of each variable, in g/ml or g/cm³, as a function of age for every combinations of sex and APOE4 status for our standard model.

Figure 3

Concentrations of intracellular Aβ (Aβⁱ), GSK-3 (G), phosphorylated/hyperphosphorylated tau proteins (τ), and intracellular NFTs (F_i) per unit of neuron density for our standard model.

Figure 4

Rate of neuronal death in 1/day or g/cm³/day (= g/ml/day), as a function of age, for different combinations of sex and APOE4 status with the standard model. (A) Women, APOE4−; (B) Women, APOE4+; (C) Men, APOE4−; (D) Men, APOE4+.

Figure 5

Activation rates of microglia, in g/cm³/day, as a function of age for different combinations of sex and APOE4 status. (A) Women, APOE4−; (B) Women, APOE4+; (C) Men, APOE4−; (D) Men, APOE4+. Observe that the M_activ curve is very close to the one “M_activ by F_o”.

Figure 6

Concentration of each variable, in g/ml or g/cm³, as a function of age for every combinations of sex and APOE4 status for the model with constant insulin concentration.

Figure 7

Concentration of each variable, in g/ml or g/cm³, as a function of age, for APOE+ women, for the standard model (black), and the model with constant insulin concentration (orange).

Figure 8

Concentration of intracellular Aβ (Aβⁱ), GSK-3, phosphorylated/hyperphosphorylated tau proteins (τ), and intracellular NFTs (F_i) normalized by the density of neurons, for the model with constant insulin concentration.

Figure 9

Concentration of each variable, in g/ml or g/cm³, as a function of age, for every combinations of sex and APOE4 status, for the model with reduced microglia activation rates (κ_FoM × 0.5 et ${\kappa }_{{A\beta }_o^{o}M}\times 0.5$).

Figure 10

Concentration of intracellular Aβ (Aβⁱ), GSK-3, phosphorylated/hyperphosphorylated tau proteins (τ), and intracellular NFTs (F_i) normalized by the density of neurons for the model with reduced microglia activation rate (κ_FoM × 0.5 and ${\kappa }_{{A\beta }_o^{o}M}\times 0.5$). The curves for GSK3/N and τ/N for the same sex overlap.

Figure 11

Concentration of each variable, in g/ml or g/cm³, as a function of age for APOE+ women, for the standard model (ξ = 1) and for the model with reduced microglia activation rate (ξ = 0.8, 0.5 and 0.3) (κ_FoM × ξ and ${\kappa }_{{A\beta }_o^{o}M}\times \xi$).

Figure 12

Microglia activation rates in g/cm³/day, as a function of age for different combinations of sex and APOE4 status for the model with reduced microglia activation rate: κ_FoM × 0.5 and ${\kappa }_{{A\beta }_o^{o}M}\times 0.5$ (ξ = 0.5). (A) Women APOE4−; (B) Women, APOE4+; (C) Men, APOE4−; (D) Men, APOE4+. The total activation rate M_activ is very similar to the activation rate “M_activ by F_o,” so the curves overlap.