Network Inference With the Lasso
- PMID: 38587864
- PMCID: PMC11559558
- DOI: 10.1080/00273171.2024.2317928
Network Inference With the Lasso
Abstract
Calculating confidence intervals and p-values of edges in networks is useful to decide their presence or absence and it is a natural way to quantify uncertainty. Since lasso estimation is often used to obtain edges in a network, and the underlying distribution of lasso estimates is discontinuous and has probability one at zero when the estimate is zero, obtaining p-values and confidence intervals is problematic. It is also not always desirable to use the lasso to select the edges because there are assumptions required for correct identification of network edges that may not be warranted for the data at hand. Here, we review three methods that either use a modified lasso estimate (desparsified or debiased lasso) or a method that uses the lasso for selection and then determines p-values without the lasso. We compare these three methods with popular methods to estimate Gaussian Graphical Models in simulations and conclude that the desparsified lasso and its bootstrapped version appear to be the best choices for selection and quantifying uncertainty with confidence intervals and p-values.
Keywords: bootstrap; debiased lasso; desparsified lasso; multisplit method; p-values for lasso.
Figures
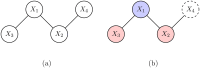
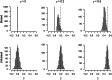
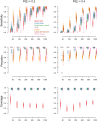
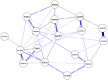

References
-
- Bertsimas, D., King, A., & Mazumder, R. (2016). Best subset selection via a modern optimization lens. The Annals of Statistics, 44(2), 813–852. 10.1214/15-AOS1388 - DOI
-
- Bilodeau, M., & Brenner, D. (1999). Theory of multivariate statistics. Springer-Verlag.
-
- Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., & Hwang, D. (2006). Complex networks: Structure and dynamics. Physics Reports, 424(4-5), 175–308. 10.1016/j.physrep.2005.10.009 - DOI
MeSH terms
LinkOut - more resources
Full Text Sources
