Nonlinear social evolution and the emergence of collective action

Abstract

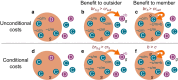
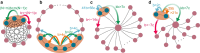
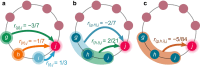
Organisms from microbes to humans engage in a variety of social behaviors, which affect fitness in complex, often nonlinear ways. The question of how these behaviors evolve has consequences ranging from antibiotic resistance to human origins. However, evolution with nonlinear social interactions is challenging to model mathematically, especially in combination with spatial, group, and/or kin assortment. We derive a mathematical condition for natural selection with synergistic interactions among any number of individuals. This result applies to populations with arbitrary (but fixed) spatial or network structure, group subdivision, and/or mating patterns. In this condition, nonlinear fitness effects are ascribed to collectives, and weighted by a new measure of collective relatedness. For weak selection, this condition can be systematically evaluated by computing branch lengths of ancestral trees. We apply this condition to pairwise games between diploid relatives, and to dilemmas of collective help or harm among siblings and on spatial networks. Our work provides a rigorous basis for extending the notion of "actor", in the study of social evolution, from individuals to collectives.

Keywords: coalescent theory; collective action; evolutionary dynamics; evolutionary game theory; social evolution.

Fig. 1.

Modeling framework. a) We consider a population of alleles at a specific locus. Alleles can be of type A or a. Each allele resides in a particular genetic site, within an individual. Each time-step, some alleles are replaced by copies of others, as a result of interaction, reproduction, mating, and/or death. This is recorded in a parentage map, α, indicating the parent allele of each site in the new state. b) The process of selection is represented as a Markov chain. State transitions are determined by sampling a parentage map α from a probability distribution, which depends on the current state and captures all effects of social interaction, spatial structure, mating pattern, and so on. With mutation, there is a unique stationary distribution over states. c) Multilateral genetic assortment is quantified by collective relatedness $r_{S,g}$, which characterizes the likelihood that site g contains allele A when all sites in set S do. d) Under neutral drift, collective relatedness can be computed using the expected branch lengths, ${\ell }_S$, of the tree representing S’s ancestry. The smaller the coalescence length ${\ell }_S$, the more likely that sites in S contain the same allele.

Fig. 2.

Collective Action dilemma. A collective S, of size m, may help or harm a target g. There are two heritable strategies: (C)ontribute or (D)o not contribute. If all members of S contribute, g receives benefit b; otherwise no benefit is received. a) For unconditional costs, each Contributor in S pays cost $c/m$. b) Applying Eq. 10, selection favors collective action if $b{r}_{S,g}>c{r}_{\mathrm{self}}$. c) If the target g belongs to S, then $r_{S,g}$ is replaced by S’s intrarelatedness $r_S$. d) Conditional costs are only paid if the benefit would be achieved. e) Action is favored if $b{r}_{S,g}>c{r}_S$. f) If the target belongs to S, the condition becomes $b{r}_S>c{r}_S$, which reduces to $b>c$.

Fig. 3.

Collective action on networks. We analyze the Collective Action Dilemma, with unconditional costs, on a fixed network of size N. a) In a well-mixed population, represented by a complete graph, a collective of size m is favored to help a member if $(N-m)b>m(N-1)c$, and favored to harm an outsider if $b<-(N-1)c$. b) For a large ($N\gg 1$) cycle network, a connected collective of four or more nodes is favored to help its own boundary nodes if $b>2c$, and the neighbors of these boundary nodes if $b>4c$; neither help nor harm are favored to other nodes. c) On a windmill network with $k\gg 1$ blades, a blade is favored to help the hub if $kb>7c$. This can occur even if the benefit is a small fraction of the cost. In contrast, help to a node within the blade is only favored if $41b>56c$. Harmful behavior is favored toward nodes in other blades if $b<-14c$. d) The “spider” network displays similar behavior, but help is more readily favored to the inner node of a leg ($25b>21c$) than to the outer node ($b>2c$). Results in panels b–d refer to large populations ($N\gg 1$); results for finite N are derived in SI Appendix, Sections 9.5–9.7, and shown in Fig. S1.

Fig. 4.

Collective action on spatial networks. a–b) Delaunay networks (78) are a model of 2D spatial structure, formed by randomly placing points in a square and joining neighbors together. We identified network subcommunities using a spatial variant of the Girvan–Newman algorithm (79) (SI Appendix, Section 9.8.1). We then computed the cost–benefit thresholds ${\kappa }_{S,g}$, in the Collective Action Dilemma, from each subcommunity S to each target node g. Collective action is favored if $b{\kappa }_{S,g}>c$; larger values indicate greater propensity for action (positive for help, negative for harm). These are compared to the corresponding well-mixed thresholds, $\kappa =(N-m)/(m(N-1))$ for members and $\kappa =-1/(N-1)$ for outsiders, to determine the effects of network structure. c) We generated 50 Delaunay networks of size 16, comprising 298 subcommunities. Spatial structure promotes help, in the sense ${\kappa }_{S,g}>(N-m)/(m(N-1))$, to 86% of internal targets. The remaining 14% tend to be further inside the collective, away from the boundary. (Percentages exclude “collectives” of size one, which necessarily have ${\kappa }_{S,g}=1$ to their one member.) d) Spatial structure promotes help (${\kappa }_{S,g}>0$) to 17% of external targets, of which 94% of which are neighbors of the collective and the rest are two-step neighbors. Harm is promoted (${\kappa }_{S,g}<-1/(N-1)$) to the majority of external targets. Selection for costly help or harm to outsiders decreases with collective size.

Fig. 5.

Conflicting inclusive fitness interests within a collective. Suppose the fitness of a site j depends on the alleles in three others, g, h, and i. Eq. 10 then has three terms arising from single sites, $c_{\{g\},j}{r}_{\{g\},j}+c_{\{h\},j}{r}_{\{h\},j}+c_{\{i\},j}{r}_{\{i\},j}$, three from pairwise synergistic effects, $c_{\{g,h\},j}{r}_{\{g,h\},j}+c_{\{g,i\},j}{r}_{\{g,i\},j}+c_{\{h,i\},j}{r}_{\{h,i\},j}$, and one, $c_{\{g,h,i\},j}{r}_{\{g,h,i\},j}$, from all three together. a) If g, h, i, and j are consecutive nodes on a cycle of size 8, then i is positively related to j, indicating potential for helpful behavior, while g and h are negatively related to j, indicating potential for harm. b) The collective $\{h,i\}$ is positively related to j, while $\{g,h\}$ is negatively related to j. c) Together, $\{g,h,i\}$ are negatively related to j. The outcome of selection reflects an aggregation over these individual and collective interests.