Hamiltonian energy in a modified Hindmarsh-Rose model

Abstract

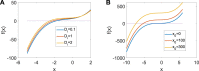
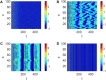
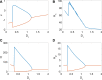
This paper investigates the Hamiltonian energy of a modified Hindmarsh-Rose (HR) model to observe its effect on short-term memory. A Hamiltonian energy function and its variable function are given in the reduced system with a single node according to Helmholtz's theorem. We consider the role of the coupling strength and the links between neurons in the pattern formation to show that the coupling and cooperative neurons are necessary for generating the fire or a clear short-term memory when all the neurons are in sync. Then, we consider the effect of the degree and external stimulus from other neurons on the emergence and disappearance of short-term memory, which illustrates that generating short-term memory requires much energy, and the coupling strength could further reduce energy consumption. Finally, the dynamical mechanisms of the generation of short-term memory are concluded.

Keywords: HR; Turing instability; delay; matrix; network; pattern formation.

FIGURE 1

Distribution of the equilibrium point in system (3) when a = | 1, b = | 3, c = | 1, d = | 5, r = | 0.01, s = | 4. (A) Distribution of the equilibrium point when x ₀ | = | 1. (B) Distribution of the equilibrium point when D _i = | 1.

FIGURE 2

Pattern formation when I _ext = | 4 and W (100, | 8, | 0.01). (A) Pattern formation when d ₁ | = | 0.01. (B) Pattern formation when d ₁ | = | 0.05. (C) Pattern formation when d ₁ | = | 0.3. (D) Pattern formation when d ₁ | = | 1.

FIGURE 3

Pattern formation when I _ext = | 4, d ₁ | = | 1 and W (100, K, | 0.01). (A) Pattern formation when K = | 0. (B) Pattern formation when K = | 2. (C) Pattern formation when K = | 4. (D) Pattern formation when K = | 6.

FIGURE 4

Hamiltonian energy, change in Hamiltonian energy, and membrane potential when I _ext = | 1, x ₀ | = | 1. (A) Evolution when D _i = | 0.1. (B) Evolution when D _i = | 1. (C) Evolution when D _i = | 1.5.

FIGURE 5

Average Hamiltonian energy, average change in Hamiltonian energy, and membrane potential when I _ext = | 1. (A) Bifurcation of membrane potential. (B) Average Hamiltonian energy. (C) Max–min value of Hamiltonian energy. (D) Max–min value of Hamiltonian energy variation.

FIGURE 6

Hamiltonian energy, change in Hamiltonian energy, and membrane potential when D _i = | 0.1, I _ext = | 1. (A) Evolution when x ₀ | = | 5. (B) Evolution when x ₀ | = | 10. (C) Evolution when x ₀ | = | 20. (D) Evolution when x ₀ | = | 200.

FIGURE 7

Average Hamiltonian energy, change in Hamiltonian energy, and membrane potential when D _i = | 1, I _ext = | 1. (A) Bifurcation of membrane potential. (B) Average Hamiltonian energy. (C) Max–min value of Hamiltonian energy. (D) Max–min value of Hamiltonian energy variation.