The bistable mitotic switch in fission yeast

Abstract

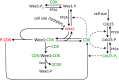
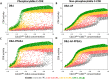
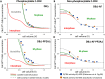
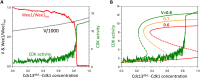
In favorable conditions, eukaryotic cells proceed irreversibly through the cell division cycle (G1-S-G2-M) in order to produce two daughter cells with the same number and identity of chromosomes of their progenitor. The integrity of this process is maintained by "checkpoints" that hold a cell at particular transition points of the cycle until all requisite events are completed. The crucial functions of these checkpoints seem to depend on irreversible bistability of the underlying checkpoint control systems. Bistability of cell cycle transitions has been confirmed experimentally in frog egg extracts, budding yeast cells and mammalian cells. For fission yeast cells, a recent paper by Patterson et al. (2021) provides experimental evidence for an abrupt transition from G2 phase into mitosis, and we show that these data are consistent with a stochastic model of a bistable switch governing the G2/M checkpoint. Interestingly, our model suggests that their experimental data could also be explained by a reversible/sigmoidal switch, and stochastic simulations confirm this supposition. We propose a simple modification of their experimental protocol that could provide convincing evidence for (or against) bistability of the G2/M transition in fission yeast.

FIGURE 1:

The molecular regulatory network of the model. Wee1 (red) represents the active forms of both Wee1 and Mik1 kinases. Active CDK (green) is inhibited by phosphorylation by Wee1 and reactivated by Cdc25 phosphatase (the active form is green). Wee1 forms a stoichiometric complex with CDK before catalyzing its inhibitory phosphorylation. The Wee1:CDK dimer can be attacked by active CDK to phosphorylate Wee1 and release two CDKs. Both Wee1 and Cdc25 are doubly phosphorylated by CDK, and the phosphorylations are reversed by PP2A. Because the active form of Wee1 is unphosphorylated and the active form of Cdc25 is doubly phosphorylated, the net activation of CDK is governed by two interlocked, positive feedback loops. Total Cdc25 concentration increases as the cell grows. Cell growth inhibits “Wee1” because the synthesis of Mik1 is restricted to small cells early in the cell cycle.

FIGURE 2:

Stochastic simulations of the bistable mitotic-switch model. CDK activity is plotted as a function of fusion-protein concentration (#molec/V, V in arbitrary units) after induction of Cdc13^dbΔ-Cdk1 (left column: A and C) and Cdc13^dbΔ-Cdk1^AF (right column: B and D) in pp2a⁺ (top row: A and B) and pp2aΔ-deleted background (bottom row: C and D). Cells are sorted into four cell size bins (V = 1000 corresponds roughly to a dividing wildtype cell of length 14 μm and volume 100 fL).

FIGURE 3:

Dose-response curves for the dependence of the CDK-activity sensor on fusion-protein concentration predicted by the deterministic model. CDK-activity sensor is plotted as a function of fusion-protein concentration after induction of Cdc13^dbΔ-Cdk1 (left column: A and C) and Cdc13^dbΔ-Cdk1^AF (right column: B and D) in pp2a⁺ (top row: A and B) and pp2aΔ-deleted background (bottom row: C and D). CDK activities are plotted for fixed values of the parameter V in the deterministic model that corresponds to the middle of the cell-size bins defined for the stochastic simulations.

FIGURE 4:

Cell-size dependence of fusion-protein thresholds for mitotic entry and exit in the deterministic model. Induction of Cdc13^dbΔ-Cdk1 (left column: A and C) and Cdc13^dbΔ-Cdk1^AF (right column: B and D) in pp2a⁺ (top row: A and B) and pp2aΔ-deleted background (bottom row: C and D). Solid lines depict the saddle-node bifurcation points for transitions into M phase (green line) and back to interphase (red line). Grey dashed lines depict the fusion protein concentration where CDK activity reaches the value of five. Orange circles and blue squares show fusion protein concentrations where more than 50% of cells have CDK activity higher than five in our stochastic simulations and in the experiments of Patterson et al. (2021), respectively.

FIGURE 5:

Comparison of the stochastic and deterministic models. (A) Stochastic simulation of mitotic entry induced by fusion protein in WT genetic background for a cell born with volume = 600. (B) Overlay of a stochastic simulation on a one-parameter bifurcation diagram comparable to Figure 3A.

FIGURE 6:

The reversible mitotic-switch model. (A and C) Stochastic simulations of Cdc13^dbΔ-Cdk1 induction in pp2a⁺ and pp2aΔ-deleted backgrounds, respectively. (B and D) Cell size dependence of fusion-protein threshold for mitotic entry in pp2a⁺ and pp2aΔ-deleted backgrounds, respectively. The dashed grey lines depict where CDK activity = 5 in the deterministic model. The orange circles and blue squares indicate the fusion-protein concentrations where more than 50% of cells have CDK activity higher than five in our stochastic simulations and in Patterson et al. (2021) experiments, respectively.

FIGURE 7:

Reversibility of mitotic entry and exit in a monostable, ultrasensitive mitotic-switch model. (A) The dependence of fusion-protein thresholds on cell size. The dashed line depicts the fusion-protein concentration where CDK activity = 5 in our deterministic model. The triangles (▴ and ▾) indicate the fusion-protein concentrations where more than 50% of cells have CDK activity higher and lower than five, respectively, in our stochastic simulations. (B–D) Stochastic simulations of dialing-up the concentration of Cdc13^dbΔ-Cdk1 (red, yellow and green data points) and dialing-down the concentration of degradable Cdc13-Cdk1 fusion-protein (grey data points). Cells are clustered according to size into small (panel B, V = 650–800), medium (panel C, V = 800–950) and large (panel D, V = 950–1100) size classes. During dialing-up, nondegradable C-CDK is induced for different times in cells that are initially in the low CDK activity state (interphase); during dialing-down, the level of degradable C-CDK is followed in cells that are initially in the high CDK activity state (M-phase) and are degrading the fusion protein.

FIGURE 8:

Hysteresis in the bistable mitotic-switch model. (A) The dependence of fusion-protein thresholds on cell size. The green and red lines are the saddle-node bifurcation points in our deterministic model where CDK activity abruptly rises and falls, respectively. The triangles (▴ and ▾) indicate fusion-protein concentrations where more than 50% of cells have CDK activity higher and lower than five, respectively, in our stochastic simulations. (B–D) Stochastic simulations of mitotic entry (dialing-up) and exit (dialing-down) with stable (Cdc13^dbΔ-Cdk1) and unstable (Cdc13-Cdk1) fusion-protein, respectively. Cells are clustered according to their size into small (panel B, V = 650–800), medium (panel C, V = 800–950) and large (panel D, V = 950–1100) classes. During dialing-up, nondegradable C-CDK is induced for different times in cells that are initially in the low CDK activity state (interphase); during dialing-down, the concentration of degradable C-CDK is followed in cells that are initially in the high CDK activity state (M-phase) and are degrading the fusion protein.