Rarefied gas flow in functionalized microchannels

Abstract

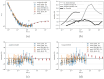
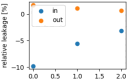
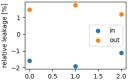
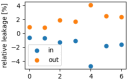
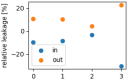
The interaction of rarefied gases with functionalized surfaces is of great importance in technical applications such as gas separation membranes and catalysis. To investigate the influence of functionalization and rarefaction on gas flow rate in a defined geometry, pressure-driven gas flow experiments with helium and carbon dioxide through plain and alkyl-functionalized microchannels are performed. The experiments cover Knudsen numbers from 0.01 to 200 and therefore the slip flow regime up to free molecular flow. To minimize the experimental uncertainty which is prevalent in micro flow experiments, a methodology is developed to make optimal use of the measurement data. The results are compared to an analysis-based hydraulic closure model (ACM) predicting rarefied gas flow in straight channels and to numerical solutions of the linearized S-model and BGK kinetic equations. The experimental data shows that if there is a difference between plain and functionalized channels, it is likely obscured by experimental uncertainty. This stands in contrast to previous measurements in smaller geometries and demonstrates that the surface-to-volume ratio of 0.4 $\mu$ m ${}^{-1}$ seems to be too small for the functionalization to have a strong influence and highlights the importance of geometric scale for surface effects. These results also shed light on the molecular reflection characteristics described by the TMAC.

Keywords: BGK equations; Carbon dioxide; Gas separation membranes; Knudsen number; Mesopores; S-model; TMAC.

Figure 1

Channel sockets for (a) the IUSTI experimental facility and (b) the TRANSFLOW experimental facility.

Figure 2

(a) The functionalization setup. (b) Evaluation of functionalization by contact angle measurement (white) with water. Left: the plain channel. Right: the channel with HDTMS functionalization.

Figure 3

Schematic view of the experimental setups. During an experiment, valve B is closed for the IUSTI setup and open for the TRANSFLOW setup. Valve A is closed in both setups.

Figure 4

(a) Experimental facility TRANSFLOW. (b) Experimental facility at the IUSTI laboratory.

Figure 5

Depiction of two time windows. A time window is defined by a start and a width. One window consists of the data with white background. Another window consists of the data with white and light grey background: it has an earlier start and a larger width.

Figure 6

Differences between mass flow rates calculated from upstream and downstream pressure changes. Each square corresponds to a fragment of the data defined by its corresponding window start and window width. The lower right part is empty because the window would end outside the available data. This results in (50x50)/2 = 1250 single evaluations. Some samples at the top are empty because no fit for that data was found. (a) The full array without any threshold. (b) A threshold of 8 %; only very few fragments fulfill this threshold. No sufficiently large area can be found. (c) A threshold of 10%. More fragments fulfill this threshold, but not enough to find a sufficiently large area. (d) A threshold of 10.7% results in a structure where a sufficiently large area can be found (marked with a circle). Therefore, the corresponding relative uncertainty of mass flow rate due to the data fragment method is 5.35%.

Figure 7

(a) Dimensionless mass flow rate obtained experimentally (symbols) and calculated from the analysis-based hydraulic closure model (ACM) (line). The outlier in grey color is not included in further analysis. (b) Deviation of the ACM analytical model and the linearized S-model from the linearized BGK model. (c) Comparison of experiments to the ACM analytical model. A negative value corresponds to an experimental value smaller than the analytical one. (d) Comparison of experiments to the numerical solution of the linearized BGK equation.

Figure 8

T-test confidence intervals with a 95% confidence level depicting the means and standard deviations of the centers and width of the intervals resulting from the Monte Carlo sampling (a) for the analysis-based hydraulic closure model (ACM) baseline and (b) for the linearized BGK model baseline.

Figure 9

Relative leakage of |D2_CO2_1000_100_leakage_07-12-21|.

Figure 10

Relative leakage of |D2_He_1000_100_leakage_10k_14-01-22|.

Figure 11

Relative leakage of |D2_He_100_100_leakage_1700_18-01-22|.

Figure 12

Relative leakage of |D2_He_1000_1000_leakage_42k_08-02-22|.

Figure 13

Relative leakage of |C2_He_100_100_leakage_700_18-03-22|.

Figure 14

Relative leakage of |C2_CO2_100_100_leakage_14-03-22|.

Figure 15

Deviations of experimental data from the solution of the linearized BGK equation. (a) Helium and carbon dioxide in plain channels. (b) Helium and carbon dioxide in functionalized channels. (c) Helium in plain and functionalized channels. (d) Carbon dioxide in plain and functionalized channels.

Figure 16

(a) Comparison of experiments to the ACM analytical model. A negative value corresponds to an experimental value smaller than the analytical one. (b) Comparison of experiments to the numerical solution of the linearized S-model equation. (c) Comparison of experiments to the numerical solution of the linearized BGK equation.