A Predictive Model for the Evolution of COVID-19

Abstract

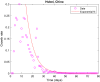
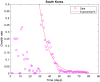
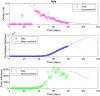
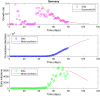
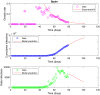
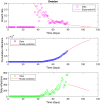
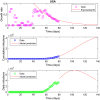
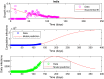
We predict the evolution of the COVID-19 pandemic in several countries using a logistic model. The model uses a regression analysis based on the least-squares fitting. In particular, the growth rate of the infection has been fitted as an exponential decay, as compared to a linear decay, reported previously in logistic models. The model has been validated with the data of China and South Korea, where the pandemic is nearing to its end. The data of Italy, Germany, Spain, and Sweden show that the peak of the infection has been reached, i.e. a time when the new infections will start to decrease as compared to the previous day. The model predicts the approximate number of total infections at the end of the outbreak. The possible peak date and the total number of infections for different countries are predicted using the data available. The total number of infections in the USA is estimated to be around 4 million. The model prediction of Brazil shows that the peak will reach on 5 July 2020 and total infections will be 3.2 million. The reported data of India show a large initial scatter in the growth rate. The total number of infections in India is estimated to be around 2.4 million by the model and the predicted peak date is 3 August 2020. The predictions of India are discussed in the context of restricted movement of population, i.e. lock-down imposed by the government.

Keywords: COVID-19; Epidemiology; Logistic model.

Fig. 1

Validation of the model with data of Hubei, China. Day 0 is 22 January 2020. The growth rate is seen as an exponential decay, well predicted by the model fit

Fig. 2

Validation of the model for South Korea. Rest of the caption is same as of Fig. 1

Fig. 3

Data and model forecast for Italy. Day 0 is 22 January 2020 and data until 10 April 2020 is analysed. Time-history of the growth rate of the infections per day (top row), cumulative number of infections (middle row) and daily infections (bottom row) are plotted. The data are shown by symbols while the solid lines are predicted from the model. Simulation is stopped if ${\lambda }_{t_i}\le 0.01$ or the change in total infections per day is lesser than 1%

Fig. 4

Data and model forecast for Germany. Rest of the caption is same as of Fig. 3

Fig. 5

Data and model forecast for Spain. Rest of the caption is same as of Fig. 3

Fig. 6

Data and model forecast for Sweden. Rest of the caption is same as of Fig. 3

Fig. 7

Data and model forecast for USA. Rest of the caption is same as of Fig. 3

Fig. 8

Data and model forecast for Brazil. Day 0 is 22 Jan 2020, and data until 31 May 2020 are analyzed. Time-history of the growth rate of the infections per day (top row), cumulative number of infections (middle row) and daily infections (bottom row) are plotted. The data are shown by symbols while the solid lines are predicted from the model. Simulation is stopped if ${\lambda }_{t_i}\le 0.001$ or the change in total infections per day is lesser than 0.1%

Fig. 9

Data and model forecast for India. Rest of the caption is the same as of Fig. 8