Computationally Efficient Demographic History Inference from Allele Frequencies with Supervised Machine Learning
- PMID: 38636507
- PMCID: PMC11082913
- DOI: 10.1093/molbev/msae077
Computationally Efficient Demographic History Inference from Allele Frequencies with Supervised Machine Learning
Abstract
Inferring past demographic history of natural populations from genomic data is of central concern in many studies across research fields. Previously, our group had developed dadi, a widely used demographic history inference method based on the allele frequency spectrum (AFS) and maximum composite-likelihood optimization. However, dadi's optimization procedure can be computationally expensive. Here, we present donni (demography optimization via neural network inference), a new inference method based on dadi that is more efficient while maintaining comparable inference accuracy. For each dadi-supported demographic model, donni simulates the expected AFS for a range of model parameters then trains a set of Mean Variance Estimation neural networks using the simulated AFS. Trained networks can then be used to instantaneously infer the model parameters from future genomic data summarized by an AFS. We demonstrate that for many demographic models, donni can infer some parameters, such as population size changes, very well and other parameters, such as migration rates and times of demographic events, fairly well. Importantly, donni provides both parameter and confidence interval estimates from input AFS with accuracy comparable to parameters inferred by dadi's likelihood optimization while bypassing its long and computationally intensive evaluation process. donni's performance demonstrates that supervised machine learning algorithms may be a promising avenue for developing more sustainable and computationally efficient demographic history inference methods.
Keywords: demographic history inference; machine learning; population genomics.
© The Author(s) 2024. Published by Oxford University Press on behalf of Society for Molecular Biology and Evolution.
Figures
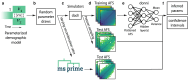

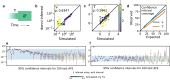

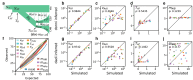
Update of
-
Computationally efficient demographic history inference from allele frequencies with supervised machine learning.bioRxiv [Preprint]. 2024 Feb 15:2023.05.24.542158. doi: 10.1101/2023.05.24.542158. bioRxiv. 2024. Update in: Mol Biol Evol. 2024 May 3;41(5):msae077. doi: 10.1093/molbev/msae077. PMID: 38405827 Free PMC article. Updated. Preprint.
References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

