Enhanced Photo-excitation and Angular-Momentum Imprint of Gray Excitons in WSe2 Monolayers by Spin-Orbit-Coupled Vector Vortex Beams

Abstract

A light beam can be spatially structured in the complex amplitude to possess orbital angular momentum (OAM), which introduces an extra degree of freedom alongside the intrinsic spin angular momentum (SAM) associated with circular polarization. Furthermore, superimposing two such twisted light (TL) beams with distinct SAM and OAM produces a vector vortex beam (VVB) in nonseparable states where not only complex amplitude but also polarization is spatially structured and entangled with each other. In addition to the nonseparability, the SAM and OAM in a VVB are intrinsically coupled by the optical spin-orbit interaction and constitute the profound spin-orbit physics in photonics. In this work, we present a comprehensive theoretical investigation, implemented on the first-principles base, of the intriguing light-matter interaction between VVBs and WSe₂ monolayers (WSe₂-MLs), one of the best-known and promising two-dimensional (2D) materials in optoelectronics dictated by excitons, encompassing bright exciton (BX) as well as various dark excitons (DXs). One of the key findings of our study is that a substantial enhancement of the photoexcitation of gray excitons (GXs), a type of spin-forbidden DX, in a WSe₂-ML can be achieved through the utilization of a 3D-structured TL with the optical spin-orbit interaction. Moreover, we show that a spin-orbit-coupled VVB surprisingly allows for the imprinting of the carried optical information onto GXs in 2D materials, which is robust against the decoherence mechanisms in the materials. This suggests a promising method for deciphering the transferred angular momentum from structured light to excitons.

Keywords: WSe2; gray exciton; transition-metal dichalcogenide; twisted light; two-dimensional materials; vector vortex beam.

Figure 1

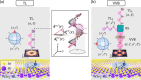
(a) Schematic of a single TL in the state |σ, ⟩ normally incident on a WSe₂ monolayer (WSe₂-ML), where σ and represent the SAM and OAM carried by the TL, respectively. The panel on the right-hand side shows that the polarization of a TL (pink arrow line) is not purely transverse (gray arrow line), , but also contains a small longitudinal field component (red arrow line), , resulting from the optical SOI. Below the TL, the small square panel displays the contour plot of the squared magnitude of the longitudinal component of the vector potential and the in-plane circular polarizations (white arrow lines) of the TL, where the polarization remains fixed over the in-plane. The schematic on the left-hand side illustrates that the TL state, |σ, ⟩, is located at the north pole of the Poincaré sphere. (b) Schematic of a VVB superimposed by two TLs, |σ, ⟩ and |σ′, ′⟩, normally incident on a WSe₂-ML. BS stands for beam splitter. Below the VVB, the small square panel displays the contour plot of the squared magnitude of the longitudinal component of the vector potential and the in-plane polarizations of the VVB, both of which are spatially varied, unlike a TL. The VVB here is a state located at the equator of the Poincaré sphere, i.e., |σ, , σ′, ′⟩ ≡ |σ, , σ′, ′; α = 0, β = π/2⟩ (see eq 1 for the definition).

Figure 2

(a) Spin-resolved quasi-particle band structure of a WSe₂-ML calculated by using the first-principles package Quantum Espresso with the PBE functional in DFT. The color of bands is mapped to the spin z-component of the Bloch states, , where σ_z is the Pauli matrix. The left inset shows the first Brillouin zone of TMD-MLs. The dashed rectangular box is the enlarged view of the lowest spin-split conduction bands and the topmost valence band at K-valley, where the green arrow line indicates the transitions of spin-allowed BX, the blue arrow line indicates the transition of spin-forbidden GX and DX, and the tilted arrow line indicates the transition of the exciton with a finite center-of-mass momentum, Q. (b) Calculated 1s-exciton band structure, on the Q_x-axis, of a WSe₂-ML sandwiched by semi-infinite hBN layers obtained by solving the first-principles-based BSE, comprising the valley-split BX states, |B±, Q⟩, and the lowest GX and DX states, |G, Q⟩ and |D, Q⟩. The exciton bands are offset by the energy of BX at Q = 0. The gradient green colors of the exciton states are mapped to the in-plane component of the transition dipole of exciton, |D_S,Q^X,∥|. (c) shows the same exciton band structure as (b) but presents the out-of-plane component of the transition dipoles, |D_S,Q^X,z|, using gradient blue colors.

Figure 3

(a) Exciton fine structure of the low-lying exciton states along the Q_x axis around the vicinity of the light-cone reciprocal range, comprising the valley-split BX bands (green circles) and the lowest GX (blue circles) and DX ones (black circles). Q_c = E_B±,0^X/ℏc is defined as the light-cone radius. For comparison, the band dispersions of BX states simulated by using the pseudospin model (red line) that considers a fixed value for the dipole of BX are presented. (b1)–(b3) Density plots of the optical transition rates as functions of Q for the finite momentum BX states of a WSe₂-ML under the excitation of polarized TLs with the SAM and OAM, (σ, ) = (±1, 0), (±1, 5), and (±1, 15), respectively. (c1)–(c3) Density plots of for the TL-excited finite-momentum GX states. All of the contour plots follow the same color-map on the leftmost side. For reference, the length of the horizontal bar in white color represents the magnitude of 0.1Q_c. (d) Total transition rates of the TL-excited superposition states of BX (empty green squares) and GX states (empty blue squares) as a function of the of the TL, calculated by taking the exciton band structure obtained by solving the first-principles-based BSE from (a). For a more realistic simulation, the effective refractive index of TMD-MLs,n_rf = 4.8, that shortens the wavelength of light in materials (q₀ → n_rfq₀ and Q_c → n_rfQ_c) is considered for comparison, as illustrated by the empty green and blue diamonds for BXs and GXs, respectively. In model simulations, where a fixed dipole value is assumed, the results for n_rf = 1 and n_rf = 4.8 are shown by the filled and empty red circles, respectively.

Figure 4

Representation of higher-order Poincaré sphere for the superposition states, |σ, , σ′, ′; α, β⟩, of VVBs in the basis of the two TLs with and . (a) Density plots of the squared magnitudes of the transverse components of the vector potentials, , for the VVB states at the poles and equator of higher-order Poincaré sphere over the q_∥-plane. For reference, the length of the horizontal bar in white color represents the magnitude of q_∥ = 0.1Q_c. (b) Density plots of the squared magnitudes of the longitudinal components of the vector potentials, , of the same VVBs as presented in (a). While the pattern of always remains isotropic as varying the geometric angles of the superposition states of VVB, those of of the equatorial superposition states exhibit anisotropic patterns, possessing the rotational symmetry associated with the finite ≠ 0 carried by the TL basis of the VVB. The dark circular panels in (a,b) present the spatially varying transverse polarizations of the VVBs over the q_∥-plane. The pure states of TL basis at the poles (β = 0, π) possess circular polarization. By contrast, the maximal superposition states of VVB at the equatorial points (β = π/2) are linearly polarized along the direction depending on q_∥.

Figure 5

(a) Density plots of the Q-dependent transition rates, Γ_B,Q^{1,1,–1,–1}(α,β), of the finite-momentum BX doublet, |B±,Q⟩, and (b) Q-dependent transition rates, Γ_G,Q^{1,1,–1,–1}(α,β), of the finite-momentum GX state, |G, Q⟩, under the excitation of the VVBs in the TL-superposition states, |1, 1, −1, −1; α, β⟩, with the different geometric angles, (α, β) = (0, 0), (0, π), (0, π/2), and (π, π/2), in the higher order Poincaré sphere representation. The schematic inset in each panel illustrates the optical transition corresponding to each case. For reference, the length of the horizontal bar in white color represents the magnitude of Q = 0.1Q_c. 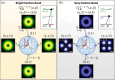Notably, Γ_G,Q^{1,1,–1,–1}(α, β = π/2) exhibits the anisotropic patterns with the fourfold rotation symmetry (n = 4), from which the angular momentum, and ′(=–), carried by the TL basis can be inferred according to eq 10.

Figure 6

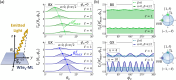
Angle-dependent optical transition rate, Γ_S(θ_ν, ϕ_ν), of the BX doublet and GX states excited by the -encoded VVB and single TL. (a) θ_ν-dependence of the transition rate, Γ_S(θ_ν, ϕ_ν = 0), for the BX (upper) and GX states (lower) photoexcited by the -encoded VVB state |σ, , −σ, −; α, β⟩ along the x–z plane (ϕ_ν = 0). Note that the polar angle, , for the maximum transition rate increases with the increasing value of in the VVB. The schematic on the left-hand side illustrates the polar, θ_ν, and azimuthal angle, ϕ_ν, of the light emitted from a WSe₂-ML. (b) ϕ_ν-dependence of the transition rate, , for the BX (upper) and GX states (lower) exited by the -encoded single TL (i.e., the state with β = 0 on the Poincaré sphere) and VVB with (α = 0, β = π/2) at . Note that the ϕ_ν-dependence of the transition rate of the GX states mainly follow the n-fold patterns appeared in the ϕ_Q-dependence of the transition rates in Figure 5b.