An evaluation of synthetic data augmentation for mitigating covariate bias in health data

Abstract

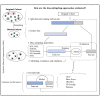
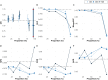
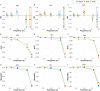
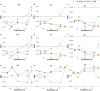
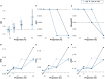
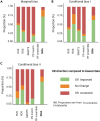
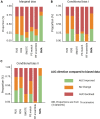
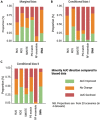
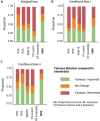
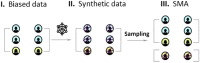
Data bias is a major concern in biomedical research, especially when evaluating large-scale observational datasets. It leads to imprecise predictions and inconsistent estimates in standard regression models. We compare the performance of commonly used bias-mitigating approaches (resampling, algorithmic, and post hoc approaches) against a synthetic data-augmentation method that utilizes sequential boosted decision trees to synthesize under-represented groups. The approach is called synthetic minority augmentation (SMA). Through simulations and analysis of real health datasets on a logistic regression workload, the approaches are evaluated across various bias scenarios (types and severity levels). Performance was assessed based on area under the curve, calibration (Brier score), precision of parameter estimates, confidence interval overlap, and fairness. Overall, SMA produces the closest results to the ground truth in low to medium bias (50% or less missing proportion). In high bias (80% or more missing proportion), the advantage of SMA is not obvious, with no specific method consistently outperforming others.

Keywords: classification; covariate imbalance; data bias; fairness; generative model; synthetic data generation.

Graphical abstract

Figure 1

Bias type Simulations results across 500 iterations for the full model showing the impact of bias (increasing missing proportion) on (A) odds ratio (OR) and the standard deviation of the biasing covariate across simulation runs, (B) the overall area under the curve (AUC), (C) minority-group AUC, and fairness metrics: (D) statistical parity difference (SPD), (E) equal opportunity difference (EOD), and (F) average odds difference (AOD). The dashed line represents the ground truth from the original data.

Figure 2

Bias mitigation approach Simulations results across 500 iterations for the full model showing the comparisons of the OR estimates and the standard deviation of the biasing covariate across simulation runs (A–C), overall model AUCs (D–F), and minority-group AUC of the biasing covariate (G–I) for synthetic minority augmentation (SMA), random oversampling (ROS, the best-performing alternative), and biased data. The dashed line represents the ground truth from unbiased data.

Figure 3

Bias mitigation approach Simulation results across 500 iterations for the full model showing the fairness estimates based on (A–C) statistical parity difference (SPD), (D–F) equal opportunity difference (EOD), and (G–I) average odds difference (AOD). The estimates are reported for biased data, ROS (the best-performing alternative), and SMA. The dashed line represents the optimal fairness value under no data bias.

Figure 4

Bias type Impact of bias (increasing missing proportion) on the CCHS data in evaluating the (A) odds ratio (OR) and standard error of the biasing covariate, (B) the overall AUC, (C) minority-group AUC, and three fairness metrics: (D) statistical parity difference (SPD), (E) equal opportunity difference (EOD), and (F) average odds difference (AOD). The bias is assessed under marginal bias (MB), conditional bias I (CBI), and conditional bias II (CBII). The dashed line represents the ground-truth results in the original dataset.

Figure 5

Bias mitigation approach Comparisons on the CCHS dataset of the OR estimates with and standard error of the biasing covariate (A–C), overall model AUCs (D–F), and minority-group AUC of the biasing covariate (G–I) for SMA, random oversampling (ROS, the best-performing alternative), and biased data. The dashed line represents the ground truth from unbiased data.

Figure 6

Bias mitigation approach Fairness metrics on the CCHS dataset: (A–C) the statistical parity difference (SPD), (D–F) equal opportunity difference (EOD), and (G–I) average odds difference (AOD) from the logistic regression model on the cardiovascular health data. The proportion of samples removed varied from 15% to 80%. Original cohort: SPD = 0.096, EOD = 0.092, and AOD = 0.098. The symbol ǂ indicates that the estimates are averaged from m = 100 synthetic copies. The dashed line represents the ground-truth fairness in the original dataset.

Figure 7

Summaries of the OR of the biasing covariate for the four real datasets The relative performance of each bias-mitigating approach compared to the biased data estimate is shown. The OR direction is considered improved if the difference between the model OR and the ground-truth estimate is less than the difference between the biased data OR and the ground truth. Summaries are over all four datasets, and proportions range from 15% to 80%.

Figure 8

Summaries of the model AUC for the four real datasets The relative performance of each bias-mitigating approach compared to biased data results is shown. The model AUC is considered improved if the difference between the model AUC and the ground-truth estimate is less than the difference between the biased data AUC and the ground truth. Summaries are over all four datasets, and proportions range from 15% to 80%.

Figure 9

Summaries of the minority-group AUC over the four real datasets The relative performance of each bias-mitigating approach compared to biased data results is shown. The minority AUC is considered improved if the difference between the model minority AUC and the ground-truth estimate is less than the difference between the biased data minority AUC and the ground truth. Summaries are over all bias proportions: 15%, 30%, 50%, 80%, and 95%.

Figure 10

Summaries of the fairness metrics SPD, EOD, and AOD over the four real datasets The relative performance of each bias-mitigating approach compared to biased data results is shown. Fairness is considered improved if the difference between the model fairness and the ground-truth estimate is less than the difference between the biased data fairness and the ground truth. Summaries are over all four datasets, and proportions range from 15% to 80%.

Figure 11

A schematic for synthetic data augmentation from biased data From (I) to (II), a synthetic version of the biased data is generated. In step (III), the synthetic minority group is sampled from (II) and augmented with the biased data in (I) to generate a rebalanced dataset.

Figure 12

Illustration of the synthesis process for a four-variable dataset

Figure 13

Schematic for training and evaluating bias-mitigating approaches