Epidemiological feature analysis of SVEIR model with control strategy and variant evolution

Abstract

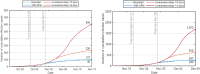
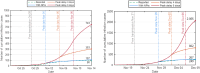
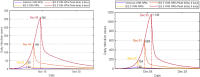
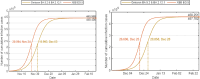
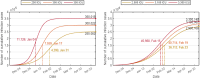
The complex interactions were performed among non-pharmaceutical interventions, vaccinations, and hosts for all epidemics in mainland China during the spread of COVID-19. Specially, the small-scale epidemic in the city described by SVEIR model was less found in the current studies. The SVEIR model with control was established to analyze the dynamical and epidemiological features of two epidemics in Jinzhou City led by Omicron variants before and after Twenty Measures. In this study, the total population (N) of Jinzhou City was divided into five compartments: the susceptible (S), the vaccinated (V), the exposed (E), the infected (I), and the recovered (R). By surveillance data and the SVEIR model, three methods (maximum likelihood method, exponential growth rate method, next generation matrix method) were governed to estimate basic reproduction number, and the results showed that an increasing tendency of basic reproduction number from Omicron BA.5.2 to Omicron BA.2.12.1. Meanwhile, the effective reproduction number for two epidemics were investigated by surveillance data, and the results showed that Jinzhou wave 1 reached the peak on November 1 and was controlled 7 days later, and that Jinzhou wave 2 reached the peak on November 28 and was controlled 5 days later. Moreover, the impacts of non-pharmaceutical interventions (awareness delay, peak delay, control intensity) were discussed extensively, the variations of infection scales for Omicron variant and EG.5 variant were also discussed. Furthermore, the investigations on peaks and infection scales for two epidemics in dynamic zero-COVID policy were operated by the SVEIR model with control. The investigations on public medical requirements of Jinzhou City and Liaoning Province were analyzed by using SVEIR model without control, which provided a possible perspective on variant evolution in the future.

Keywords: COVID-19; Control strategy; SVEIR model; Twenty measures; Variant evolution.

Fig. 1

Flow diagram of the disease transmission.

Fig. 2

Numerical simulation for Jinzhou wave 1 (L) and Jinzhou wave 2 (R) in Jinzhou City.

Fig. 3

Changes in Rt for Jinzhou wave 1 (L) and Jinzhou wave 2 (R) in Jinzhou City.

Fig. 4

Infection scales of Jinzhou wave 1 (L) and Jinzhou wave 2 (R) by SVEIR model with awareness delay.

Fig. 5

Infection scales of Jinzhou wave 1 (L) and Jinzhou wave 2 (R) by SVEIR model with peak delay.

Fig. 6

Infection scales of Jinzhou wave 1 (L) and Jinzhou wave 2 (R) by SVEIR model with control intensity.

Fig. 7

Daily infection cases led by EG.5 variant against Omicron variant for Jinzhou wave 1 (L) and Jinzhou wave 2 (R) during dynamic zero-COVID policy.

Fig. 8

Daily infection cases and cumulative infection cases of Jinzhou wave 1 (L) and Jinzhou wave 2 (R) without NPIs.

Fig. 9

Simulations of ICU beds requirements for Jinzhou City (L) and Liaoning Province (R).