All-Atom Photoinduced Charge Transfer Dynamics in Condensed Phase via Multistate Nonlinear-Response Instantaneous Marcus Theory
- PMID: 38657208
- PMCID: PMC11099976
- DOI: 10.1021/acs.jctc.4c00010
All-Atom Photoinduced Charge Transfer Dynamics in Condensed Phase via Multistate Nonlinear-Response Instantaneous Marcus Theory
Abstract
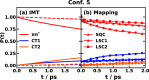
Photoinduced charge transfer (CT) in the condensed phase is an essential component in solar energy conversion, but it is challenging to simulate such a process on the all-atom level. The traditional Marcus theory has been utilized for obtaining CT rate constants between pairs of electronic states but cannot account for the nonequilibrium effects due to the initial nuclear preparation. The recently proposed instantaneous Marcus theory (IMT) and its nonlinear-response formulation allow for incorporating the nonequilibrium nuclear relaxation to electronic transition between two states after the photoexcitation from the equilibrium ground state and provide the time-dependent rate coefficient. In this work, we extend the nonlinear-response IMT method for treating photoinduced CT among general multiple electronic states and demonstrate it in the organic photovoltaic carotenoid-porphyrin-fullerene triad dissolved in explicit tetrahydrofuran solvent. All-atom molecular dynamics simulations were employed to obtain the time correlation functions of energy gaps, which were used to generate the IMT-required time-dependent averages and variances of the relevant energy gaps. Our calculations show that the multistate IMT could capture the significant nonequilibrium effects due to the initial nuclear state preparation, and this is corroborated by the substantial differences between the population dynamics predicted by the multistate IMT and the Marcus theory, where the Marcus theory underestimates the population transfer. The population dynamics by multistate IMT is also shown to have a better agreement with the all-atom nonadiabatic mapping dynamics than the Marcus theory does. Because the multistate nonlinear-response IMT is straightforward and cost-effective in implementation and accounts for the nonequilibrium nuclear effects, we believe this method offers a practical strategy for studying charge transfer dynamics in complex condensed-phase systems.
Conflict of interest statement
The authors declare no competing financial interest.
Figures

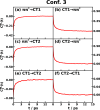

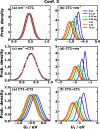
 of CPC60 triad conformation
3 for different transitions j → k obtained from all-atom equilibrium MD simulations on the Vj potential surface at 300
K.
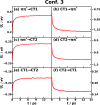
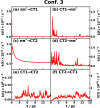
of CPC60 triad conformation
3 for different transitions j → k obtained from all-atom equilibrium MD simulations on the Vj potential surface at 300
K.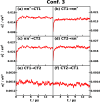
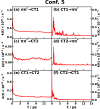
 of CPC60 triad conformation
3 for different transitions j → k obtained from all-atom equilibrium MD simulations on the Vj potential surface at 300
K.
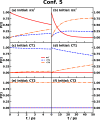
of CPC60 triad conformation
3 for different transitions j → k obtained from all-atom equilibrium MD simulations on the Vj potential surface at 300
K.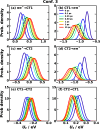


Similar articles
-
Instantaneous Marcus theory for photoinduced charge transfer dynamics in multistate harmonic model systems.J Phys Condens Matter. 2024 May 7;36(31). doi: 10.1088/1361-648X/ad42f2. J Phys Condens Matter. 2024. PMID: 38657642
-
Linear-Response and Nonlinear-Response Formulations of the Instantaneous Marcus Theory for Nonequilibrium Photoinduced Charge Transfer.J Chem Theory Comput. 2021 Apr 13;17(4):2065-2079. doi: 10.1021/acs.jctc.0c01250. Epub 2021 Mar 9. J Chem Theory Comput. 2021. PMID: 33687212
-
Photoinduced Charge Transfer Dynamics in the Carotenoid-Porphyrin-C60 Triad via the Linearized Semiclassical Nonequilibrium Fermi's Golden Rule.J Phys Chem B. 2020 Oct 29;124(43):9579-9591. doi: 10.1021/acs.jpcb.0c06306. Epub 2020 Oct 15. J Phys Chem B. 2020. PMID: 33059444
-
Path Integrals for Nonadiabatic Dynamics: Multistate Ring Polymer Molecular Dynamics.Annu Rev Phys Chem. 2022 Apr 20;73:299-322. doi: 10.1146/annurev-physchem-082620-021809. Epub 2022 Jan 26. Annu Rev Phys Chem. 2022. PMID: 35081325 Review.
-
Nonadiabatic Dynamics Simulations for Photoinduced Processes in Molecules and Semiconductors: Methodologies and Applications.J Chem Theory Comput. 2023 Dec 12;19(23):8491-8522. doi: 10.1021/acs.jctc.3c00960. Epub 2023 Nov 20. J Chem Theory Comput. 2023. PMID: 37984502 Review.
Cited by
-
Revisiting the Marcus inverted regime: modulation strategies for photogenerated ultrafast carrier transfer from semiconducting quantum dots to metal oxides.RSC Adv. 2025 Jul 28;15(33):26897-26918. doi: 10.1039/d5ra04311e. eCollection 2025 Jul 25. RSC Adv. 2025. PMID: 40727290 Free PMC article. Review.
-
Nonadiabatic Field: A Conceptually Novel Approach for Nonadiabatic Quantum Molecular Dynamics.J Chem Theory Comput. 2025 Apr 22;21(8):3775-3813. doi: 10.1021/acs.jctc.5c00181. Epub 2025 Apr 7. J Chem Theory Comput. 2025. PMID: 40192130 Free PMC article. Review.
References
-
- Wang J.; Cui Y.; Chen Z.; Zhang J.; Xiao Y.; Zhang T.; Wang W.; Xu Y.; Yang N.; Yao H.; Hao X.-T.; Wei Z.; Hou J. A Wide Bandgap Acceptor with Large Dielectric Constant and High Electrostatic Potential Values for Efficient Organic Photovoltaic Cells. J. Am. Chem. Soc. 2023, 145, 13686–13695. 10.1021/jacs.3c01634. - DOI - PubMed
LinkOut - more resources
Full Text Sources
