Postural Change of the Annual Cicada (Tibicen linnei) Helps Facilitate Backward Flight

Abstract

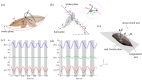
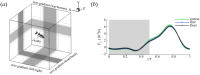
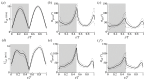
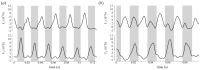
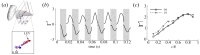
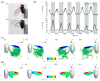
Cicadas are heavy fliers well known for their life cycles and sound production; however, their flight capabilities have not been extensively investigated. Here, we show for the first time that cicadas appropriate backward flight for additional maneuverability. We studied this flight mode using computational fluid dynamics (CFD) simulations based on three-dimensional reconstructions of high-speed videos captured in a laboratory. Backward flight was characterized by steep body angles, high angles of attack, and high wing upstroke velocities. Wing motion occurred in an inclined stroke plane that was fixed relative to the body. Likewise, the directions of the half-stroke-averaged aerodynamic forces relative to the body (local frame) were constrained in a narrow range (<20°). Despite the drastic difference of approximately 90° in body posture between backward and forward flight in the global frame, the aerodynamic forces in both flight scenarios were maintained in a similar direction relative to the body. The forces relative to the body were also oriented in a similar direction when observed during climbs and turns, although the body orientation and motions were different. Hence, the steep posture appropriated during backward flight was primarily utilized for reorienting both the stroke plane and aerodynamic force in the global frame. A consequence of this reorientation was the reversal of aerodynamic functions of the half strokes in backward flight when compared to forward flight. The downstroke generated propulsive forces, while the upstroke generated vertical forces. For weight support, the upstroke, which typically generates lesser forces in forward flight, is aerodynamically active in backward flight. A leading-edge vortex (LEV) was observed on the forewings during both half strokes. The LEV's effect, together with the high upstroke velocity, increased the upstroke's force contribution from 10% of the net forces in forward flight to 50% in backward flight. The findings presented in this study have relevance to the design of micro-aerial vehicles (MAVs), as backward flight is an important characteristic for MAV maneuverability or for taking off from vertical surfaces.

Keywords: aerodynamic force control; backward flight; body kinematics; cicada; insect maneuverability.

Figure 1

The cicada in free flight. (a) Experimental setup showing the filming arrangement with high-speed cameras. (b) Cicada (Tibicen linnei) image and template (shown in green) with relevant labels. LE—leading edge, TE—trailing edge, FW—forewing, HW—hindwing, C is the mid-span chord, L is the body length, R is the wing length. (c) Reconstructed cicada template overlapped on the cicada in free flight.

Figure 2

Relevant definitions. (a) Wing Euler angle definitions. (b) Wing chord at 0.75R. US—blue, DS—red. Measured wing kinematics of (c) CCD #1 and (d) CCD #2 based on the definitions in (a). The solid and dashed lines represent the forewing and hindwing measurements, respectively. (e) ${\widehat{e}}_1$, ${\widehat{e}}_2$, and $\widehat{n}$ are are orthonormal and form the basis of the local/body coordinate frame. The angle between the half-stroke-averaged aerodynamic force $\left(\overline{F}\right)$ and body normal $\left(\widehat{n}\right)$ is denoted as μ, X, Y, and Z form the basis for the global coordinate frame.

Figure 3

CFD simulation setup. (a). Computational domain with boundary conditions. For display, the meshes were coarsened 9, 6, and 3 times in the x, y, and z directions, respectively. (b) Grid refinement. The vertical force during the second flapping stroke of CCD #1 is shown. Gray shading denotes the DS. ‘Fine’ grids are shown in (a).

Figure 4

Body kinematics. (a) Montage of flight sequences of (i) CCD #1 and (ii) CCD #2. The transparent cicadas in (i) denote the flight phases preceding backward flight (takeoff and pitch-up) of CCD #1. The white dashed lines in (i,ii) qualitatively denote the stroke plane orientation. (b) Body angle and (c) center of mass displacements and velocity of CCD #1. (d) Body angle and (e) center of mass displacements and velocity of CCD #2.

Figure 5

Additional forewing kinematics parameters. (a) Effective wing tip speed, (b) geometric AoA at 0.75R, and (c) effective AoA at 0.75R for CCD #1. (d–f) CCD #2′s data. Solid and dashed lines represent the mean ± standard deviation of all of the complete wingbeats, respectively. Gray shading denotes the DS.

Figure 6

Time history of force production in the global frame of (a) CCD #1 and (b) CCD #2. F_V—vertical force and F_H—horizontal force refer to the forces in the Y and X directions, respectively (see Figure 2a). Gray shading denotes the DS.

Figure 7

Force orientation in the global and local frames. (a,b) Half-stroke-averaged forces of CCD #1 and CCD #2, respectively, in the global frame. Red and green arrows represent ${\overline{F}}_{US}$ and ${\overline{F}}_{DS}$, respectively. The force vectors have been superimposed on the cicada at midstroke. For illustration purposes, the real spacing between each cicada model in the X-direction has been scaled up by ten chord lengths. The vector orientation, as well as the spacing in the Y-direction, were unaffected. (c,d) Orientation of the force vector relative to the body projected on the mid-sagittal plane of CCD #1 and CCD #2, respectively. $\mu$ = 0° when $\overline{F}$ is aligned in the same direction as $\widehat{n}$.

Figure 8

Flow structures visualized using the Q-criterion (Q = 600) and colored according to the pressure of the vorticial structures during the third flapping stroke of cicada #1 (t = 57–80 ms). (a) Top row (i–iv) represents snapshots during the DS at t/T = 0.13, 0.25, 0.38, and 0.48, respectively. (b) Bottom row (i–iv) denotes snapshots during the US at t/T = 0.63, 0.75, 0.88, and 0.98. The flow is colored according to the coefficient of pressure $C_p=(p-p_{\mathrm{\infty }})/0.5\rho {\overline{U}}_{eff}$. TEV—trailing-edge vortex; TV—tip vortex; RV—root vortex.

Figure 9

LEV circulation calculated for CCD #1. (a) Calculation of LEV circulation. (b) Time history of LEV circulation at the mid-span (0.50R). (c) Mean spanwise distribution of circulation at mid-stroke for all complete strokes.

Figure 10

Forewing and hindwing force generation (a). (i) Wing configuration before flight. The HW (outlined with red dashed lines) is tucked under the FW. (ii) Wing configuration in flight. The HW leading edge is connected to the FW trailing edge. (b) Force production of CCD #1. Gray shading denotes the DS. (c) Flow structures at the mid-DS (i) when the HW is present versus (ii) when the HW is absent, and at the mid-US when the HW is (iii) present versus (iv) absent. (d) Pressure differences on the wing surface at exact snapshots are shown in (c).

Figure 11

Force production and orientation in cicada flight. (a) Schematic illustrating the transition from forward to backward flight. (b) Orientation of the aerodynamic forces relative to the body normal. Data from previous research [14,15,28] are pooled together (shaded sectors on the circles). The arrows represent the data from the current study and are also shown in Figure 7.