Kelvin-Helmholtz-induced mixing in multi-fluid partially ionized plasmas

Abstract

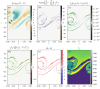
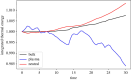
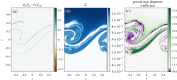
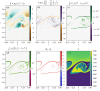
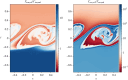
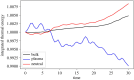
Turbulence is a fundamental process that drives mixing and energy redistribution across a wide range of astrophysical systems. For warm ([Formula: see text]) plasma, the material is partially ionized, consisting of both ionized and neutral species. The interactions between ionized and neutral species are thought to play a key role in heating (or cooling) of partially ionized plasmas. Here, mixing is studied in a two-fluid partially ionized plasma undergoing the shear-driven Kelvin-Helmholtz instability to evaluate the thermal processes within the mixing layer. Two-dimensional numerical simulations are performed using the open-source (PIP) code that solves for a two-fluid plasma consisting of a charge-neutral plasma and multiple excited states of neutral hydrogen. Both collisional and radiative ionization and recombination are included. In the mixing layer, a complex array of ionization and recombination processes occur as the cooler layer joins the hotter layer, and vice versa. In localized areas of the mixing layer, the temperature exceeds the initial temperatures of either layer with heating dominated by collisional recombinations over turbulent dissipation. The mixing layer is in approximate ionization-recombination equilibrium, however the obtained equilibrium is different to the Saha-Boltzmann local thermal equilibrium. The dynamic mixing processes may be important in determining the ionization states, and with that intensities of spectral lines, of observed mixing layers. This article is part of the theme issue 'Partially ionized plasma of the solar atmosphere: recent advances and future pathways'.

Keywords: mixing; partial ionization; shear instabilities; two-fluid.

Figure 1.

Density evolution for the simulation with collisional ionization/recombination only. Top row shows the total density (${\rho }_p+{\rho }_n$). Middle row shows the plasma density ${\rho }_p$. Lower row shows the neutral density ${\rho }_n$.

Figure 2.

Energy source terms (panels a–e) and plasma temperature (f) for the simulation using collisional ionization/recombination only. Kinetic energy and thermal energy exchange due to thermal collisions (a,b) and ionization/recombination (c,d). Panel (e) shows the net cooling/heating of the system as a result of the ionization/recombination processes. Panel (f) shows the plasma temperature.

Figure 3.

Evolution of total thermal energy through time for the plasma (blue), neutral (red) and bulk (black) fluids for the simulation using collisional rates only. Note each curve is normalized by the respective value of $t=0$.

Figure 4.

(a) Mass exchange due to ionization and recombination, (b) ionization fraction (${\xi }_i={\rho }_p/({\rho }_p+{\rho }_n)),$ (c) departure coefficient of the ground state neutral species.

Figure 5.

Density evolution for the simulation with both collisional and radiative ionization/recombination. Top row shows the total density (${\rho }_p+{\rho }_n$). Middle row shows the plasma density ${\rho }_p$. Lower row shows the neutral density ${\rho }_n$.

Figure 6.

(a–f) Energy source terms for the simulation with both collisional and radiative ionization/recombination. Here, the rates are the sum of the collisional and radiative rates.

Figure 7.

Ratio of collisional and radiative rates at time $t=24$.

Figure 8.

Evolution of the integrated thermal energy in the domain for the simulation with collisional and radiative rates. Note that each curve has been normalized by its value at time $t=0$.

Figure 9.

(a) Mass exchange due to ionization and recombination, (b) ionization fraction (${\xi }_i={\rho }_p/({\rho }_p+{\rho }_n)),$ (c) departure coefficient of the ground state neutral species.

Figure 10.

Properties from the collisional rates only simulation at time $t=24$: (a) plasma density, (b) plasma pressure, (c) magnetic pressure, (d) neutral density, (e) neutral pressure.