GraphT-T (V1.0Beta), a program for embedding and visualizing periodic graphs in 3D Euclidean space

Abstract

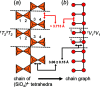
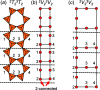
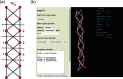
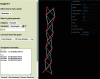
Following the work of Day & Hawthorne [Acta Cryst. (2022), A78, 212-233] and Day et al. [Acta Cryst. (2024), A80, 258-281], the program GraphT-T has been developed to embed graphical representations of observed and hypothetical chains of (SiO₄)^4- tetrahedra into 2D and 3D Euclidean space. During embedding, the distance between linked vertices (T-T distances) and the distance between unlinked vertices (T...T separations) in the resultant unit-distance graph are restrained to the average observed distance between linked Si tetrahedra (3.06±0.15 Å) and the minimum separation between unlinked vertices is restrained to be equal to or greater than the minimum distance between unlinked Si tetrahedra (3.713 Å) in silicate minerals. The notional interactions between vertices are described by a 3D spring-force algorithm in which the attractive forces between linked vertices behave according to Hooke's law and the repulsive forces between unlinked vertices behave according to Coulomb's law. Embedding parameters (i.e. spring coefficient, k, and Coulomb's constant, K) are iteratively refined during embedding to determine if it is possible to embed a given graph to produce a unit-distance graph with T-T distances and T...T separations that are compatible with the observed T-T distances and T...T separations in crystal structures. The resultant unit-distance graphs are denoted as compatible and may form crystal structures if and only if all distances between linked vertices (T-T distances) agree with the average observed distance between linked Si tetrahedra (3.06±0.15 Å) and the minimum separation between unlinked vertices is equal to or greater than the minimum distance between unlinked Si tetrahedra (3.713 Å) in silicate minerals. If the unit-distance graph does not satisfy these conditions, it is considered incompatible and the corresponding chain of tetrahedra is unlikely to form crystal structures. Using GraphT-T, Day et al. [Acta Cryst. (2024), A80, 258-281] have shown that several topological properties of chain graphs influence the flexibility (and rigidity) of the corresponding chains of Si tetrahedra and may explain why particular compatible chain arrangements (and the minerals in which they occur) are more common than others and/or why incompatible chain arrangements do not occur in crystals despite being topologically possible.

Keywords: (SiO4)4− tetrahedra; 3D Euclidean space; 3D spring-force algorithm; GraphT–T; bond topology; chains of tetrahedra; graph embedding program.

Figure 1

(a) The chain of (SiO₄)⁴⁻ tetrahedra in astrophyllite-supergroup minerals, and (b) the graphical representation of this chain (chain graph) in which tetrahedra are represented as vertices and the linkages between tetrahedra are represented as edges. Red arrows show T–T separations which are constrained to be at least 3.713 Å during embedding. Black arrows indicate T–T distances which are constrained to be 3.06±0.15 Å during embedding.

Figure 2

(a) An example of a metastable unit-distance graph in which vertex 1 occupies a false-minimum position where the 1–2 and 1–3 edges are shorter than the other (black) edges and thus vertex 1 experiences F _s in the direction of the red arrows. In response to F _s, vertex 1 also experiences F _c (black dashed arrows) as the distance between vertex 1 and all other vertices to which it is not linked is shorter than the length of the black edge. For vertex 1 to move from this false minimum, F _s must increase temporarily as shown in (b) in order to converge to the ideal position shown in (c).

Figure 3

(a) The ² T ₂ ³ T ₂ chain of (SiO₄)⁴⁻ tetrahedra in amphibole-supergroup minerals with a repeat unit that contains four tetrahedra; (b) the corresponding ² V ₂ ³ V ₂ chain graph with a repeat unit that contains four vertices; (c) another ² V ₂ ³ V ₂ chain graph that is non-isomorphic (topologically different) with the chain graph in (b).

Figure 4

(a) The Graph T–T interface showing the first few seconds of the first phase of the embedding process for a ² V ₂ ³ V ₂ unit-distance graph. (b) The unit-distance graph after 2–5 s showing rapid expansion and movement of vertices towards ideal positions with respect to the ideal T–T distances and T⋯T separations. (c) The unit-distance graph after 10–15 s where vertices occupy positions close to ideal with respect to the T–T and T⋯T constraints.

Figure 5

The Graph T–T interface showing the ² V ₂ ³ V ₂ chain in amphibole-supergroup minerals that has converged to a compatible unit-distance graph using the embedding parameters recommended by Day et al. (2024 ▸). Note the asymmetry of the hexagons at each end of the unit-distance graph due to termination effects.

Figure 6

(a) The unit-distance graph produced by embedding the chain graph shown in Fig. 3 ▸(c) in 2D. This chain is forced to curve in on itself to ensure approximately equal T–T distances. At a particular length (number of tetrahedra, n), this results in T⋯T separations that are too short (shown with a red ellipse). This unit-distance graph embedded in 3D viewed (b) along the long axis of the chain and (c) into the long axis of the chain. Note how the chain is forced to form a helical arrangement to prevent unrealistically short T⋯T separations as shown with the red ellipse in (a).

Figure 7

(a) The ⁴ V ₂ ‘shoelace’ chain graph and (b) the corresponding unit-distance graph embedded using the default embedding parameters shown in the visualization menu. Although this graph converges, it is incompatible as R〈T–T〉 and R〈T⋯T〉_min are significantly larger and smaller than the set spring length (30 Å), respectively.

Figure 8

The ⁴ V ₂ ‘shoelace’ unit-distance graph embedded using the embedding parameters recommended by Day et al. (2024 ▸). This graph converges and has T–T distances (R〈T–T〉 = 50.003–50.006 Å) in excellent agreement with the set spring length (50 Å) but is incompatible as T⋯T _min = 33.208 Å.

Figure 9

(a) The ⁴ V ₂ ‘shoelace’ unit-distance graph where R〈T–T〉 = 91.301–116.635 Å and is thus incompatible where k = 0.001 and K = −50. In an attempt to decrease R〈T–T〉, k is increased to 0.0025 and the unit-distance graph in (b) is produced where R〈T–T〉 = 74.139–91.431 Å and R〈T⋯T〉_min = 57.597–59.950 Å. Thus, one may conclude this chain graph is incompatible as any further increase in k, in an attempt to reduce R〈T–T〉, will result in a decrease in R〈T⋯T〉_min to values below γ = 58 Å. This is shown in (c) where k is increased to 0.02 and the resultant unit-distance graph does not converge.