Bayesian workflow for time-varying transmission in stratified compartmental infectious disease transmission models

Abstract

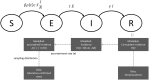
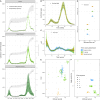
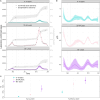
Compartmental models that describe infectious disease transmission across subpopulations are central for assessing the impact of non-pharmaceutical interventions, behavioral changes and seasonal effects on the spread of respiratory infections. We present a Bayesian workflow for such models, including four features: (1) an adjustment for incomplete case ascertainment, (2) an adequate sampling distribution of laboratory-confirmed cases, (3) a flexible, time-varying transmission rate, and (4) a stratification by age group. Within the workflow, we benchmarked the performance of various implementations of two of these features (2 and 3). For the second feature, we used SARS-CoV-2 data from the canton of Geneva (Switzerland) and found that a quasi-Poisson distribution is the most suitable sampling distribution for describing the overdispersion in the observed laboratory-confirmed cases. For the third feature, we implemented three methods: Brownian motion, B-splines, and approximate Gaussian processes (aGP). We compared their performance in terms of the number of effective samples per second, and the error and sharpness in estimating the time-varying transmission rate over a selection of ordinary differential equation solvers and tuning parameters, using simulated seroprevalence and laboratory-confirmed case data. Even though all methods could recover the time-varying dynamics in the transmission rate accurately, we found that B-splines perform up to four and ten times faster than Brownian motion and aGPs, respectively. We validated the B-spline model with simulated age-stratified data. We applied this model to 2020 laboratory-confirmed SARS-CoV-2 cases and two seroprevalence studies from the canton of Geneva. This resulted in detailed estimates of the transmission rate over time and the case ascertainment. Our results illustrate the potential of the presented workflow including stratified transmission to estimate age-specific epidemiological parameters. The workflow is freely available in the R package HETTMO, and can be easily adapted and applied to other infectious diseases.

Fig 1. Schematic overview of the SEIR transmission model for SARS-CoV-2 and the steps to generate the number of laboratory-confirmed cases and the observed seroprevalence.

Fig 2. Result from unstratified models.

(A) Posterior predictive plot for laboratory-confirmed cases (left y-axis, green ribbon) and cumulative incidence (right y-axis, gray ribbon) of SARS-CoV-2 in the canton of Geneva, Switzerland, for three iterations of the model with different sampling distributions (Poisson, quasi-Poisson and negative-binomial). Circles are weekly counts of laboratory-confirmed cases and pluses are estimates of seroprevalence at two time points. (B-D) Comparison of three methods of implementation of time-varying transmission on simulated data of a SARS-CoV-2 epidemic (posterior predictive plot, time-varying transmission ρ(t), and ascertainment rate by period). (E-F) Benchmark of different implementations of time-varying transmission on simulated data of a SARS-CoV-2 epidemic, with performance expressed in effective sample size (ESS) per second, error defined as the difference between the median posterior and true ρ(t), and the width of the 95% credible interval of ρ(t) as a measure for precision. See Table 1 for details about the knot sequence.

Fig 3. Modelled SARS-CoV-2 epidemic in Geneva, Switzerland, in 2020.

(A) Posterior predictive plot for laboratory-confirmed cases (left y-axis, colored ribbon) and cumulative incidence (right y-axis, gray ribbon) per age group. Circles are weekly counts of laboratory-confirmed cases and pluses are estimates of seroprevalence at two time points. (B) Estimates of the time-varying change in transmission rate per age group using B-splines. (C) Estimates of the ascertainment rate per age group and time period.