Impact of Beam Shape on Print Accuracy in Digital Light Processing Additive Manufacture

Abstract

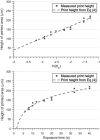
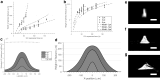
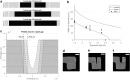
Photopolymerization-based additive manufacturing requires selectively exposing a feedstock resin to ultraviolet (UV) light, which in digital light processing is achieved either using a digital micromirror device or a digital mask. The minimum tolerances and resolution for a multilayer process are separate for resolution through the Z-axis, looking through the thickness of a printed part, and resolution in the XY-axes, in the plane of the printed layer. The former depends wholly on the rate of attenuation of the incident UV light through the material relative to the mechanical motion of the build layer, while the latter is determined by a two-dimensional pattern of irradiance on the resin formed by the digital micromirror device or the digital mask. The size or the spacing of elements or pixels of this digital mask is frequently given by manufacturers as the "resolution" of the device, however, in practice the achievable resolution is first determined by the beam distribution from each pixel. The beam distribution is, as standard, modeled as a two-parameter Gaussian distribution but the key parameters of peak intensity and standard deviation of the beam are hidden to the user and difficult to measure directly. The ability of models based on the Gaussian distribution to correctly predict the polymerization of printed features in the microscale is also typically poor. In this study, we demonstrate an alternative model of beam distribution based on a heavy-tailed Lorentzian model, which is able to more accurately predict small build areas for both positive and negative features. We show a simple calibration method to derive the key space parameters of the beam distribution from measurements of a single-layer printed model. We propose that the standard Gaussian model is insufficient to accurately predict a print outcome as it neglects higher-order terms, such as beam skew and kurtosis, and in particular failing to account for the relatively heavy tails of the beam distribution. Our results demonstrate how the amendments to the beam distribution can avoid errors in microchannel formation, and better estimates of the true XY-axes resolution of the printer. The results can be used as the basis for voxel-based models of print solidification that allow software prediction of the photopolymerization process.

Keywords: beam profiling; digital light processing; polymerization mechanics.

FIG. 1.

Overview of DLP optics in relation to build area and DMD. On the left the optical path to the build area, showing the projection of the DMD image to the build tray base. (Top right) The Z-axis resolution is primarily determined by the build layer step thickness of the build block, and by the attenuation of the UV light when printing over a void (e.g., Build Layer 3). (Bottom right) In the XY-axes, resolution is determined by the beam distribution of the DMD and projection system with each “on” pixel contributing a small amount of the total required energy for photopolymerization to take place. DLP, digital light processing; DMD, digital micromirror device; UV, ultraviolet.

FIG. 2.

Example resin model parameter estimation for PEGDA Mn250 with 0.2% wt/wt Irgacure and 0.2% wt/wt Sudan I. Print height was measured from exposure of the resin to UV light from Asiga pico HD printer with build block removed. Exposure area set by “.stl” models of a single-layer thickness and X-Y dimensions of 2 × 2 mm. The exposure time was controlled by the Asiga software with print height measured by a set of external calipers. (Top) Straight line fit to natural log of the dose (tI₀) gives the critical depth parameter as the gradient. (Bottom) Print height prediction graph for PEGDA resin with 0.2% wt/wt photoinitiator and 0.2% wt/wt Sudan I absorbent.

FIG. 3.

The method of determining the standard deviation of the pixel distribution uses a square array of single pixel filaments (a). Units in the figure are micrometers. The intensity distribution of these filaments can be measured with a CCD profiler (b) and the normalized intensity distribution curve fit to a distribution model. (c) The fit to the Gaussian and Lorentzian distributions and estimates a standard deviation of 45 μm. However, the Gaussian fit does not well predict the link between print width and print height expected from Equation 8 (d). The Lorentzian model's estimate of standard deviation (or half-width half-maximum) from measured print width is closer to the measured values (e) and predicts print width at higher exposure times much more accurately than the Gaussian model (f, g). CCD, charge-coupled device.

FIG. 4.

The measured height and width of a printed feature is plotted against exposure time for square array structures of 1, 3, and 5 pixels (a, b). In modeling the peak irradiance for a single pixel filament is less than a third of that of a 5-pixel wide filament, and less than 20% of the flat field irradiance (c). The model shape of a crossbar for 1-, 3-, and 5-pixel width (d) is presented for comparison with X-Ray images of 1-pixel- (e), 3-pixel- (f), and 5-pixel (g)-wide crossbars. Scale bars 100 μm.

FIG. 5.

Model and data on the impact of surrounding pixel intensity on microchannel formation. (a) 3-pixel channels (76 μm on the digital mask) are surrounded by walls on 10, 15, and 20 pixels. (b) A channel with designed wall widths of 10-pixels printed at increasing exposure times, compared with the printed widths from both Gaussian distribution model and Lorentzian. (c) The Lorentzian distribution model prediction of a 3-pixel channel with 10-pixel-wide walls (green), 15-pixel-wide walls (red) and 20-pixel-wide walls (blue) compared with X-ray CT scans of same channel with 10-pixel (d), 15-pixel (e), and 20-pixel walls (f). Scale bars 100 μm. CT, computer tomography.

FIG. 6.

(a) The Lorentzian model was applied to channels formed of 1-pixel gaps with 2- to 3-pixels of fractional intensity. (b) The predicted print widths for 2 columns of surrounding pixels with increasing grayscale intensity from 0 to 1.0 in intervals of 0.1 and (c) the predicted channel print for 3-pixels at 1/3 power (green), 2-pixel columns at 1/4 power (red), and 2 pixels at 1/2 power (blue) showing a failure to print. The resultant channel cross-sections are shown in (d–f). Scale bar 20 μm.

FIG. 7.

Simulation of first two build layers of an angled microchannel. The color bar scale is the degree of conversion of the material. In the top row a single exposure brings the material just to gelation point, while the second exposure increases the degree of conversion of selected parts of the first layer. Scenario (a) shows the channel overprinted in the first layer, print failure is due to overexposure. Scenario (b) shows a channel successfully printed in one layer but second layer overprints, failure is due to gradient of channel or poor match of extinction scale of light to build layer thickness. Scenario (c) shows a successful microchannel print.