Surpassing millisecond coherence in on chip superconducting quantum memories by optimizing materials and circuit design

Abstract

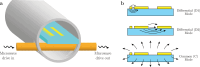
The performance of superconducting quantum circuits for quantum computing has advanced tremendously in recent decades; however, a comprehensive understanding of relaxation mechanisms does not yet exist. In this work, we utilize a multimode approach to characterizing energy losses in superconducting quantum circuits, with the goals of predicting device performance and improving coherence through materials, process, and circuit design optimization. Using this approach, we measure significant reductions in surface and bulk dielectric losses by employing a tantalum-based materials platform and annealed sapphire substrates. With this knowledge we predict the relaxation times of aluminum- and tantalum-based transmon qubits, and find that they are consistent with experimental results. We additionally optimize device geometry to maximize coherence within a coaxial tunnel architecture, and realize on-chip quantum memories with single-photon Ramsey times of 2.0 - 2.7 ms, limited by their energy relaxation times of 1.0 - 1.4 ms. These results demonstrate an advancement towards a more modular and compact coaxial circuit architecture for bosonic qubits with reproducibly high coherence.

Fig. 1. Tripole striplines in the coaxial tunnel architecture.

a Superconducting thin-film strips are patterned on a substrate and loaded into a cylindrical tunnel made of high-purity aluminum. Resonator frequencies range from 4−7 GHz (see Supplementary Table S5). A transversely oriented coupling pin is used to capacitively drive the resonators in a hanger configuration. b Cross-sectional view of the tripole stripline, showing the arrangement of the strips and electric field behaviors for each mode. While the electric field of the D1 mode is confined mostly on the surface, the electric field of the D2 mode penetrates far deeper into the bulk, rendering it sensitive to losses over a significant portion of the bulk of the substrate.

Fig. 2. Extraction of intrinsic losses with the tripole stripline.

a Power dependence of internal quality factor of the modes of a particular tripole stripline device, made using tantalum patterned on an annealed HEMEX sapphire substrate. Circles are measured Q_int; lines are TLS fits using Eq. (2). Error bars represent the propagated fit error on Q_int obtained from least-squares minimization of Eq. (9) and for some points they are small enough to not be visible. The coupling quality factors Q_c for this device are 6.3 × 10⁶, 2.2 × 10⁶, and 2.0 × 10⁶ for the D1, D2, and C modes, respectively. The relatively large error bars on the measured Q_int of the D2 and C modes (fractional errors of 7 and 17%, respectively, at single-photon powers) can be attributed to these modes being in the overcoupled regime and reduced signal-to-noise ratio at low excitation powers. b Power dependence of extracted loss factors (solid lines). The propagated error (shaded regions) for Γ_surf is small (~3%) and is hidden within the width of the solid line. Seam loss here has been normalized to be dimensionless, Γ_seam = ωϵ₀/g_seam. Γ_bulk slightly increases at intermediate photon numbers; we hypothesize that spatial inhomogeneities in TLS saturation within a single device could lead to the appearance of non-monotonicity in the extracted loss factor. c Single-photon loss budget for the modes of the tripole stripline. While the D1 mode is clearly dominated by surface loss, the D2 mode is dominated by bulk dielectric loss, and the C mode is dominated by seam loss. d, e Comparison of surface (d) and bulk (e) loss factors from multiple tripole stripline devices made using either aluminum- or tantalum-based fabrication processes on annealed (A) or unannealed (U) sapphire substrates. The device-to-device variation here captures the spatial inhomogeneity of the loss factors and their TLS properties.

Fig. 3. Prediction of transmon loss.

a 3D transmon qubit design, from which the participation ratios were calculated. Inset: SEM of Josephson junction and near-junction region on a tantalum-based transmon. Ta leads to connect to the Al junction through an overlapping Ta/Al contact region. b Predicted loss and expected T₁ for transmons made using different materials and processes (Al vs. Ta capacitor pads). The loss budget is also computed, showing the dominant sources of loss in Al- and Ta-based transmons.

Fig. 4. Predicted vs. measured transmon quality factors.

a Representative Al- and Ta-based transmon T₁ curves showing an almost factor of 2 improvement by adopting a tantalum-based process. b Measured transmon Q_int compared with predictions. Stars represent the 90th percentile transmon Q_int of a distribution formed from repeated coherence measurements over a 10-h period. Shaded regions represent a predicted range spanning one standard deviation away from predicted transmon Q_int. Measured qubit frequencies ranged from 4.5 to 6.7 GHz.

Fig. 5. Hairpin stripline quantum memory.

a Hairpin stripline quantum memory design. The ancilla transmon couples to the fundamental mode that acts as a storage resonator, and to the higher-order mode that acts as a readout resonator. A Purcell filter (meandered stripline on the left side of the chip) is used to enhance the external coupling of the readout mode. b Electric field behaviors of the memory mode (red arrows) and readout mode (green arrows). The ancilla’s capacitor pads are staggered with respect to each other to adequately couple to both modes. c Predicted loss and expected T1 for hairpin striplines made using different substrate preparations and different superconducting thin films.

Fig. 6. Hairpin stripline quantum memory coherence.

a Fock state T₁ measurement of four on-chip quantum memory devices. The Fock $∣1⟩$ state was prepared using selective number-dependent arbitrary phase (SNAP) gates and the memory state was inferred after a variable delay by selectively flipping the ancilla qubit conditioned on the memory being in the Fock $∣1⟩$ state, and measuring the ancilla state. Memory T₁’s for QM1-4 extracted by fitting an exponential to the ancilla state as a function of time were 1.05, 1.09, 1.44, and 1.14 ms. b Memory T₂ in the Fock ($∣0⟩,∣1⟩$) manifold for the four devices measured in (a). The Fock state $\frac{1}{\sqrt{2}}\left(∣0⟩+∣1⟩\right)$ was prepared using SNAP gates and after a variable delay a small displacement was applied to interfere with the memory state, followed by measurement in the same way as in (a). Ancilla state as a function of time for QM2-4 were offset vertically by 0.75, 1.5, and 2.25, respectively, for visibility, and were fit to an exponentially decaying sinusoid. Extracted memory T₂’s for QM1-4 were 2.02, 2.00, 2.68, and 2.14 ms.