Non-Poissonian Bursts in the Arrival of Phenotypic Variation Can Strongly Affect the Dynamics of Adaptation
- PMID: 38693911
- PMCID: PMC11156200
- DOI: 10.1093/molbev/msae085
Non-Poissonian Bursts in the Arrival of Phenotypic Variation Can Strongly Affect the Dynamics of Adaptation
Abstract
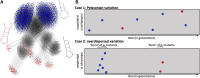
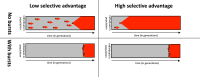
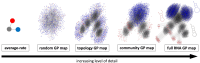
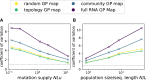
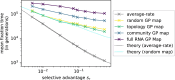
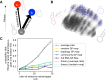
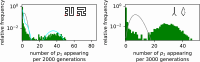
Modeling the rate at which adaptive phenotypes appear in a population is a key to predicting evolutionary processes. Given random mutations, should this rate be modeled by a simple Poisson process, or is a more complex dynamics needed? Here we use analytic calculations and simulations of evolving populations on explicit genotype-phenotype maps to show that the introduction of novel phenotypes can be "bursty" or overdispersed. In other words, a novel phenotype either appears multiple times in quick succession or not at all for many generations. These bursts are fundamentally caused by statistical fluctuations and other structure in the map from genotypes to phenotypes. Their strength depends on population parameters, being highest for "monomorphic" populations with low mutation rates. They can also be enhanced by additional inhomogeneities in the mapping from genotypes to phenotypes. We mainly investigate the effect of bursts using the well-studied genotype-phenotype map for RNA secondary structure, but find similar behavior in a lattice protein model and in Richard Dawkins's biomorphs model of morphological development. Bursts can profoundly affect adaptive dynamics. Most notably, they imply that fitness differences play a smaller role in determining which phenotype fixes than would be the case for a Poisson process without bursts.
Keywords: evolution; genotype–phenotype map; population genetics.
© The Author(s) 2024. Published by Oxford University Press on behalf of Society for Molecular Biology and Evolution.
Conflict of interest statement
Conflict of interest statement None declared.
Figures
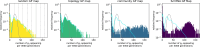
Similar articles
-
Bias in the arrival of variation can dominate over natural selection in Richard Dawkins's biomorphs.PLoS Comput Biol. 2024 Mar 27;20(3):e1011893. doi: 10.1371/journal.pcbi.1011893. eCollection 2024 Mar. PLoS Comput Biol. 2024. PMID: 38536880 Free PMC article.
-
Fitness variation across subtle environmental perturbations reveals local modularity and global pleiotropy of adaptation.Elife. 2020 Dec 2;9:e61271. doi: 10.7554/eLife.61271. Elife. 2020. PMID: 33263280 Free PMC article.
-
The arrival of the frequent: how bias in genotype-phenotype maps can steer populations to local optima.PLoS One. 2014 Feb 5;9(2):e86635. doi: 10.1371/journal.pone.0086635. eCollection 2014. PLoS One. 2014. PMID: 24505262 Free PMC article.
-
The role of robustness in phenotypic adaptation and innovation.Proc Biol Sci. 2012 Apr 7;279(1732):1249-58. doi: 10.1098/rspb.2011.2293. Epub 2012 Jan 4. Proc Biol Sci. 2012. PMID: 22217723 Free PMC article. Review.
-
Structural properties of genotype-phenotype maps.J R Soc Interface. 2017 Jul;14(132):20170275. doi: 10.1098/rsif.2017.0275. J R Soc Interface. 2017. PMID: 28679667 Free PMC article. Review.
Cited by
-
Bias in the arrival of variation can dominate over natural selection in Richard Dawkins's biomorphs.PLoS Comput Biol. 2024 Mar 27;20(3):e1011893. doi: 10.1371/journal.pcbi.1011893. eCollection 2024 Mar. PLoS Comput Biol. 2024. PMID: 38536880 Free PMC article.
References
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

