Quantum critical behavior in Ce(Fe0.76Ru0.24)2Ge2

Abstract

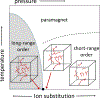
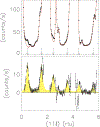
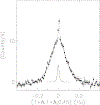
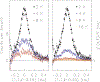
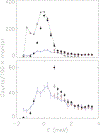
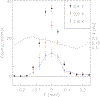
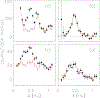
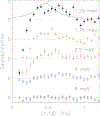
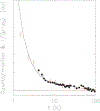
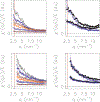
Systems with embedded magnetic ions that exhibit a competition between magnetic order and disorder down to absolute zero can display unusual low-temperature behaviors of the resistivity, susceptibility, and specific heat. Moreover, the dynamic response of such a system can display hyperscaling behavior in which the relaxation back to equilibrium when an amount of energy $E$ is given to the system at temperature $T$ only depends on the ratio $E/T$. Ce(Fe_0.755Ru_0.245)₂Ge₂ is a system that displays these behaviors. We show that these complex behaviors are rooted in a fragmentation of the magnetic lattice upon cooling caused by a distribution of local Kondo screening temperatures, and that the hyperscaling behavior can be attributed to the flipping of the total magnetic moment of magnetic clusters that spontaneously form and order upon cooling. We present our arguments based on the review of two-decades worth of neutron scattering and transport data on this system, augmented with new polarized and unpolarized neutron scattering experiments.

FIG. 1

. Putative phase diagram for a quantum critical system subject to chemical disorder. A magnetically ordered phase (grey area) can be reached by cooling down a classical system. Upon applying pressure, be it hydrostatic or chemical pressure, the transition temperature is driven down to 0 K, the quantum critical point (black dot). In the case of systems subject to chemical disorder, a distribution of Kondo-shielding temperatures will result in the formation of magnetic clusters upon cooling because of the temperature dependent moment surviving probability p. The moments within isolated clusters will line up at a temperature inversely proportional to the size of the cluster. Clusters whose moments have ordered are depicted by the jagged lines. The temperature below which isolated clusters form and order is given by the dashed line. Isolated clusters lead to the appearance of short range order, with the correlation lengths increasing the closer the QCP is approached. The lattice spanning cluster (also referred to as infinite or percolating cluster) is defined as the cluster that connects two opposite sides of the sample. In this picture, the QCP is given as the point where the infinite cluster survives down to 0 K and is about to order magnetically, resulting in long-range order.

FIG. 2.

Ce(Fe_1−xRu_x)₂Ge₂ phase diagram as a function of doping (bottom axis) and pressure (top axis). This figure has been adapted from Ref. [16]. The end compound CeRu₂Ge₂ is ferromagnetic [26] (FM) with a transition temperature of about 8 K (left axis). The other end compound CeFe₂Ge₂ is a heavy fermion system [34] (dashed-dotted vertical line). Upon replacing Ru with Fe, the FM transition temperature drops [26] (open diamonds). Once more than 50% of the Ru has been replaced with Fe the system exhibits an antiferromagnetic (AF) phase (stars) [16] and reaches a QCP at x = 0.245. Non-Fermi liquid (nFl) behavior has been observed at this concentration [20]. When the CeRu₂Ge₂ compound is subject to hydrostatic pressure (top axis), then a similar pattern is observed (curve dashed-dotted lines) [20]. Upon further increasing pressure, the system is driven through the QCP and a Fermi liquid (Fl) phase is recovered (shaded area where the resistivity exhibits a ~T² behavior [20]). Fermi liquid and Kondo shielding temperatures (filled dots) [20] for the pressurized system are displayed on the right vertical axis. All solid lines are guides to the eye.

FIG. 3.

Specific heat (a), entropy (b), susceptibility (c), and resistivity (d) for Ce(Fe_0.76Ru₂₄)₂Ge₂ measured on a piece of the single crystal used in our scattering experiments. (a) The specific heat data (open circles, top curve) were corrected for the specific heat of nonmagnetic LaFe₂Ge₂ (diamonds) to yield the magnetic specific heat (filled circles) and are plotted as c/T. The LaFe₂Ge₂ data were extrapolated from 2 K down to 0.4 K (solid line). Note the logarithmic horizontal temperature scale. (b) The c/T data were integrated numerically to yield the molar entropy S. R stands for the gas constant of 8.31 J mol⁻¹) K⁻¹. (c) The uniform susceptibility χ measured along the $c$ axis (easy axis, top curve) and along the a direction (hard direction, bottom curve). Both the horizontal and vertical axis are logarithmic axes. The solid line is $~T^{-0.6}$, the powerlaw dependence found in uniform susceptibility measurements on a piece of polycrystalline sample [16]. (d) The resistivity $\rho$ as measured along the $a$ direction (top curve) and the $c$ direction (bottom curve). The inset shows the low temperature dependence of the resistivity ${\rho }_a(T)-{\rho }_a(T=0)$. The arrows point to the onset of coherence, at around 10–15 K.

FIG. 4.

Constant q cuts through IN6 data on polycrystalline Ce(Fe_0.76Ru_0.24)₂Ge₂ at T = 1.85, 2.86, 4.36, 7.5, 10.4, 19.6, and 49.8 K as a function of energy E transferred from the neutron to the sample. The data were corrected according to Ref. [16] and have been plotted after the Bose population factor has been taken out: ${\chi }^{\prime \prime }(q,E)/E=\left(1-e^{-E/k_{B}T}\right)S(q,E)/E$ The energy resolution of the spectrometer was 0.07 meV; data within this window have not been plotted as the incoherent elastic scattering could not be sufficiently corrected for. The data at the ordering wave number $\mathrm{q}=|\overrightarrow{Q}|=3\pm 0.1{\mathrm{n}\mathrm{m}}^{-1}$ (above dotted line) display the onset of ordering upon cooling, with the additional scattering (upon cooling) exhibiting an increasingly narrow width in energy. The higher energy transfers are shown on an enlarged scale. Note that, in this energy range, there is very little temperature dependence to the data for $T<5\mathrm{K}$. The lower data set (below dotted line) is a similar cut ($q=8\pm 0.1{\mathrm{n}\mathrm{m}}^{-1}$; the data sets share the same vertical scale) but taken away from the ordering wave number. The symbols are denoted in the figure. For plotting clarity, only every other error bar has been shown.

FIG. 5.

The top panel displays the elastic HB3 scattering data on an 11 g single crystal of Ce(Fe_0.76Ru₂₄)₂Ge₂. There is a clear difference between the data measured at 2 K (points) and at 56 K (red line). Subtracting these two data sets shows the incipient order that develops (bottom panel; adapted from [28]) at the ordering wave vector $\overrightarrow{Q}=(0,0,0.45)$ as indicated by the peaks at (1,1,2n ±0.45) with n an integer (shown by arrows). Note that this signal is difficult to observe on top of the large nuclear background consisting of nuclear Bragg peaks at (1,1,2n) and aluminum powder lines. The decrease in magnetic scattering with increased momentum transfer follows the cerium form factor [28]. The filled areas under the data in the lower panel are given by a Lorentzian-line fit to the data [28].

FIG. 6.

When the lower 1-cm Ru-rich part of our single crystal of Ce(Fe_0.76Ru₂₄)₂Ge₂ is not shielded (or cut off) in elastic scattering experiments, then long-range order can be seen to develop in addition to the short-range order present in the quantum critical part of the crystal. The long-range order (at the same ordering wave vector) is seen as a resolution limited Bragg peak (dotted line) on top of the broad short-range order that was visible in Fig. 5 where the lower part of the crystal was masked. The HB3 data in the figure shown here are the differences in signal between 2 and 56 K. The negative intensities away from the ordering wave vector are caused by the diminished scattering at these wave numbers owing to Kondo shielding and a transfer of magnetic intensity from the broad background to the short-range ordered signal. The solid line through the points is a Lorentzian with full width at half maximum of 0.166 r.l.u. The stand-alone solid line is a line through the data points for the (1,1,0) nuclear Bragg peak which is shown on a different intensity scale; this Bragg peak serves as the resolution linewidth along the longitudinal direction.

FIG. 7.

Finite-size effects force the moments on an isolated cluster to line up at low temperatures. The dotted sinusoidal curve is a typical dispersion [53] for an antiferromagnetic system, displaying the energy cost (vertical axis) required to impose a disordering disturbance of wavelength $\lambda$ (horizontal axis). In here, $d$ stands for the separation between magnetic moments. Typical energy costs [53] of disturbances of wavelength $\lambda =2\mathrm{d}$, the equivalent of neighboring spins being misaligned, are of the order of a few hundred to a few thousand Kelvin. A disordering fluctuation on a cluster has the additional quantum mechanical requirement that the wavelength has to be a half-integer times the cluster diameter D: $n\lambda =2\mathrm{D}$. This requirement breaks up the continuous dispersion into a collection of points [39]. For instance, the disordering fluctuation with the longest wavelength (lowest energy) permissible on a cluster of linear size $4d$ is $\lambda =8\mathrm{d}$. This example is given by the left-most solid black dot, and its energy cost is displayed by the horizontal dashed-dotted line. The permitted wavelengths for other fluctuations on this particular cluster are shown by the other black dots. Note that a wavelength of $\lambda =\mathrm{d}$ corresponds to a fluctuation of zero energy cost since the phase difference between the moments is 360°. Thus, in order for the moments to misalign, a finite energy cost is required, dictated by the size of the cluster. If the thermal energy available is considerably less than this energy cost then clusters will be fully ordered.

FIG. 8.

Elastic scattering data obtained by subtracting the scattering measured at the temperatures shown in the figure from the data at 56 K. These data, measured on HB3 as a function of $q=(1,1,l)$, are given as the dynamic structure factor $S(q,E)$ in the left panel, and as the reduced imaginary part of the susceptibility ${\chi }^{\prime \prime }(q,E)/E=\left(1-{\mathrm{e}}^{-E/k_{B}T}\right)S(q,E)/E$ in the right panel. For elastic scattering, this conversion amounts to a division by the temperature. Note that the tails of the nuclear Bragg peak at $(\mathrm{1,1},0)$ influence and start to overwhelm the signal below $l=0.2$ (or, $l-0.45<-0.2$).

FIG. 9.

Typical raw data for our fully polarized BT7 experiment measured along (1,1,l) for the fixed energy transfers shown in the panels. The filled circles with error bars are the data measured in the spin-flip channel, the solid lines with error bars are the data in the flipper off channel. The flipper-on data in the top channel were taken at T = 50K, while the nuclear, flipper-off data are the sum over two data sets taken at 5 and 50 K. Since the latter two data sets did not differ outside of the error margins, we summed them and normalized to the monitor count. The top panel demonstrates that broad magnetic scattering is present at T = 50K. The bottom panel shows the magnetic scattering at 1.5 K, and the nuclear scattering at 5 K. When the magnetic scattering is corrected for the nonideal and time-dependent polarization efficiency [52] of the two helium-3 polarizers, then the magnetic data are given by the dashed-dotted line. The small difference between the corrected and uncorrected magnetic data demonstrates that our magnetic signal is largely free from unwanted nuclear scattering at E = 1.25meV. The peak at l = 0.67 r.l.u. in the top panel is a spurion (see Appendix).

FIG. 10.

Raw data for our unpolarized HB3 experiment measured at $\overrightarrow{q}=(0.6,0.6,0.9)$ as a function of neutron energy transfer. The filled circles are data at 1.5 K, the open symbols are data at 45 K. This figure serves as a corollary to Fig. 9: we chose a point in q space away from ordering and away from spurions. The data can be seen to obey detailed balance, proving that we are looking at true sample scattering rather than scattering by the sample environment. The data extend (at least) up to 5 meV, well beyond the scale expected for the quasielastic signal associated with Kondo shielded moments. The average Kondo temperature of our system is roughly 5–10 K (based on the temperature dependence of the quasielastic linewidth observed in the scattering by the polycrystalline sample away from ordering [16]), although the first effects of the wider distribution are already seen at higher temperatures: up to T = 20K [16] in polycrystalline data and around 10–15 K in the onset of coherence effects in the resistivity (see Appendix). Had the scattering away from ordering been associated with Kondo-shielded moments then a large difference between the data well below and well above the Kondo temperature would have been expected. Such a difference is absent in this figure at energy transfers exceeding the Kondo scale. For reference, 5 meV corresponds to a temperature of 58 K through E = k_BT.

FIG. 11.

Both panels display the energy $E$ and temperature dependence of the scattering measured at $\overrightarrow{Q}=(1,1,0.45)$ using the BT7 spectrometer in full polarization mode. The bottom panel is an enhanced vertical scale of the top panel. The filled circles are data measured in the spin flip channel at 1.56 K, the open circles at 5 K, the open diamonds at 20 K, and the line with error bars are the data at 50 K. The dashed-dotted line with the asterisks symbols are the non-spin-flip scattering data taken at 1.56 K. This latter data set is used in the correction procedure to correct for the seep-through of the nuclear scattering into the magnetic spin-flip scattering channel. The messy nuclear data serve as a reminder of how difficult it is to measure the very weak magnetic ordering signal. The peak at E = −1.5meV in the nuclear data results in a slight overcorrecting of the magnetic signal when doing the polarization correction. The bottom panel shows that the magnetic scattering increases with decreasing temperature for all energy transfers E > 0meV with the caveat that the error bars are too large for E > 2meV to draw detailed conclusions.

FIG. 12.

The temperature dependent elastic scattering near $\overrightarrow{Q}=(1,1,0.45)$. as measured on DCS. The filled circles are measured at 0.4 K (top set of points), the stars at 0.9 K, the diamonds at 1.8 K and the open circles (bottom set of points) at 56 K. The data are the raw data normalized to the incident beam monitor and summed over the energy range −0.075 < E < 0.075meV. The l values are shown on the horizontal axis, while the h and k values are given at the top of the figure. The data show that the scattering at increasingly lower temperatures appears above the already existing scattering levels. Note that because the amount of momentum transferred along all crystallographic axes varies for each data point, we cannot conclude anything about the line shape other than that magnetic Bragg peaks do not appear down to 0.4 K, indicating that the sample remains in the (nominally) paramagnetic phase.

FIG. 13.

The net scattering data measured on DCS at the ordering wave vector $\overrightarrow{Q}=(1,1,0.45)$ are shown for three temperatures (indicated in the figure). The data in the figure were obtained by grouping the scattering data in energy bins 0.04 meV wide (taking the center of the bin as the energy values displayed in the figure). The binned data were then summed over 0.99 r.l.u. < h,k < 1.01 r.l.u., and the signal at 56 K was subtracted from all three datasets shown in the figure. Since q and E vary for each data point, the value of l displays an energy dependence. This energy dependence is shown by the dashed-dotted line and the vertical scale on the right hand side. The line drawn through the T = 1.8K points simply connects the data points. It can be seen from the figure that the additional scattering that develops below 1 K is restricted to energies $E$ with |E| < 0.1meV. The data are slightly asymmetric around E = 0 because of the asymmetric Ikeda-Carpenter type resolution function [54] characteristic of time-of-flight spectrometers, moving the scattering to lower energy transfers and producing a negative energy tail. The characteristic half width at half height of the scattering at 0.4 K is 0.05 meV, which is the energy resolution of the DCS spectrometer. Note that the scattering for E > 0.1meV is significantly different from zero (implying there is more scattering at these temperatures than at T = 56K), and that this scattering is virtually independent of temperature, suggesting that clusters that form below 2 K do not fluctuate on the timescales less than 80 ps.

FIG. 14.

The temperature dependence of the scattering at $\overrightarrow{Q}=$ (1,1,0.45) as measured on TRIAX, HB3, and BT7 for the elastic channel E = 0meV, and for the inelastic channel at E = 1.25meV. For all instruments, the latter energy transfer is sufficiently far removed from E = 0 that resolution broadened elastic scattering is not measured. The symbols used are clarified in the figure legend. The vertical scale is different between all four data sets. In order to tease out the differences in the temperature dependence, we subtracted the scattering at the highest temperature so that the solid horizontal line measures the scattering with respect to the level at 100 K. We then placed the elastic HB3 and TRIAX scattering data on the same level by multiplying the TRIAX scattering by a constant factor, chosen the achieve the best agreement between the two datasets over as large a temperature range as possible. This establishes the temperature dependence of the elastic scattering. Note that the TRIAX experiment was set up to measure this critical scattering with high accuracy (despite the more limited temperature range that could be achieved), as opposed to the HB3 experiment that had a different primary purpose. The same holds true for the inelastic data where the TRIAX data are more accurate than the BT7 data, but the BT7 data extended to lower temperatures. The inelastic data were put on the same scale the same way as the elastic data, and in addition, the inelastic data sets were multiplied by a constant factor so that the temperature dependence of the elastic and inelastic data would be similar over the largest range possible. When all is set and done, the data show that the temperature dependence of the elastic and inelastic data are qualitatively different, with the differences appearing below T < 10K.

FIG. 15.

The width in reciprocal space for short-range order scattering at E = 0 meV (top) and at E = 1.25 meV (bottom panels) as measured on BT7. (a) and (c) display the spin-flip scattering data measured along (1,1,l) at 1.56 K (filled symbols) and at 50 K (open symbols with line connecting the points). The difference between the low and high temperatures are shown in panels (b) and (d) as filled symbols. The solid lines in panels (b) and (d) are best fits to a Lorentzian line with full width at half maximum of (0.17 ± 0.02) r.l.u. [(b) for E = 0meV] and (0.33 ± 0.05) r.l.u. [(d) for E = 1.25meV]. See Appendix for a discussion on the spurious bump at l = 2/3 r.l.u. The data at the lowest l in (a) show the seep-through of the strong nuclear Bragg peak at (1,1,0). While the polarization correction procedure removes most of the nuclear scattering, it is not 100% effective. Similarly, the data at T = 50K in (c) at the lowest l values appear to show some temperature dependent nuclear scattering (phonons). As such, the lowest l data should be taken with a grain of salt, representing the limits of what polarizers can correct for when flipper off data are not taken at each and every corresponding temperature because of beam time restrictions.

FIG. 16.

The net neutron scattering counts at 4.5 K as measured on TRIAX after subtraction of the counts at 80 K. The data are obtained as a function of momentum transfer along (1,1,l) for fixed energies shown in the figure. Each energy panel is offset along the vertical axis for clarity, with the dotted lines representing zero net counts. While the data show that there is more scattering at 4.5 K than at 80 K around the ordering wave vector for energy transfers up to 4 meV, the data are too noisy to determine the width in reciprocal space. The solid line in the 1.25-meV data panel is the best fit from the NIST data at the same energy and 1.56 K (see Fig. 15). The main problem in doing the temperature based subtraction in unpolarized experiments is the temperature dependence of the phonon scattering associated with the (1,1,0) nuclear Bragg peak. This problem manifests itself as a negative phonon peak located at (q, $E$) points determined by the phonon dispersion.

FIG. 17.

Comparison between the resistivity and the elastic scattering at the ordering wave vector as measured on HB3 (squares) and TRIAX (filled circles). The neutron scattering data are plotted with respect to their level at 100 K (solid horizontal line) and the TRIAX data were multiplied by a constant factor identical to Fig. 14. The solid line through the points is the measured conductance along the (1,1,0) direction plotted as 1/(ρ − ρ₀) with respect to the value at 100 K of this quantity. These data were then multiplied with a constant factor chosen to achieve the visually best correspondence with the neutron scattering data. The temperature is displayed on a logarithmic scale. When comparing to Fig. 14 we see that the resistivity data follow the elastic scattering data that, in turn, were shown to exhibit a much more rapid increase below 8 K than the data at 1.25 meV that increased much more gradually.

FIG. 18.

Cuts through IN6 data on polycrystalline Ce(Fe_0.76Ru_0.24)₂Ge₂ at T = 1.85, 2.86, 4.36, 7.5, 10.4, 19.6, and 49.8 K. The solid lines in the top left panel show the traces of representative detectors through reciprocal space. The three boxes represent the cuts at constant energy (0 ± 0.1, 0.5 ± 0.3, 1.25 ± 0.3 meV). The results of these cuts are shown in the bottom left, top right and bottom right panels, respectively. The vertical line at q = 2.7 nm⁻¹ is given by $\mathrm{q}=|\overrightarrow{Q}|$. The data were corrected according to the procedure described in ref. [16], which includes a direct subtraction of the scattering at 150 K in the range |E| < 0.1meV. The data are shown as,${\chi }^{\prime \prime }(q,E)/E$ implying that the Bose population factor has been taken out. The various temperatures are denoted by the symbols “+” (1.85 K), stars (2.86 K), diamonds (4.86 K), triangles (7.5 K), squares (10.4 K), “x” (19.6 K), and circles (49.8 K). The elastic cut in the lower left panel shows the rapid (with temperature) increase in scattering at the ordering wave number. The occasional negative intensities are the result of having subtracted the elastic scattering at 150 K. The cuts at 0.5 and 1.25 meV demonstrate that there is very little temperature evolution below 5 K other than the Bose population changes, and that the characteristic width (in q) of these cuts is significantly larger than the width at E = 0meV. Note that the three panels do not share an identical vertical scale; only the datasets within the same panel share the same vertical scale. For plotting clarity only every third error bar is shown.

FIG. 19.

Cuts through IN6 data on polycrystalline heavyfermion (HF) CeFe_1.7Ru_0.3Ge₂ at T = 1.85, 4.38, 7.5, 10.5, 19.7, and 49.8 K (left two panels). The top left panel was taken at E = 0.5 ± 0.3meV, the bottom left panel at E = 1.25 ± 0.3meV. The cuts were performed identical to the ones on the quantum critical (QCP) sample shown in Fig. 18. The various temperatures are denoted by the symbols “+” (1.85 K), stars (4.38 K), diamonds (7.5 K), triangles (10.5 K), squares (19.7 K), and “x” (49.8 K). The two panels on the right compare cuts through the quantum critical sample (filled symbols) to cuts through the heavy fermion sample (open symbols). The top right panel shows cuts at E = 0.5 ± 0.3meV for T = 1.86K (HF sample) and 7.5 K (QCP sample) [top two curves] and for T = 7.5K (HF sample) and T = 15.1K (QCP sample) [bottom two curves]. The cuts for the different samples at different temperatures demonstrate a large degree of similarity. The lower right panel compares the cuts at E = 1.25 ± 0.3meV for T = 1.86 (HF sample) and 4.36 K (QCP sample) (top two curves) and for T = 10.5 (HF sample) and 15.1 K (QCP sample) (bottom two curves). Note that the four panels do not share an identical vertical scale; only the data sets within the same panel share the same vertical scale. For plotting clarity only every third error bar is shown.

FIG. 20.

The single crystal [50] of Ce(Fe_0.76Ru_0.24)₂Ge₂ used for all single-crystal neutron scattering experiments. The part labeled “bottom” exhibited long-range order (see Fig. 6) and was part of the first HB3 experiments, subsequently masked with Gd paint for follow-up HB3 experiments, and cut off in later experiments (DCS, TRIAX, BT7). The part labeled “top” was cut off and used in specific heat, susceptibility, and resistivity measurements.

FIG. 21.

Mircroprobe measurements reveal the presence of a Ge-rich secondary phase as white lines. These two photos (showing different magnification) were taken using the bottom section of the crystal.