Temperature Sensitivity of 14N- V and 15N- V Ground-State Manifolds
- PMID: 38716475
- PMCID: PMC11070733
- DOI: 10.1103/PhysRevApplied.19.064084
Temperature Sensitivity of 14N- V and 15N- V Ground-State Manifolds
Abstract
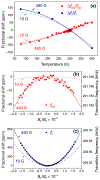
We measure electron- and nuclear-spin transition frequencies in the ground state of nitrogen-vacancy (N-V) centers in diamond for two nitrogen isotopes (14N-V and 15N-V) over temperatures ranging from 77 to 400 K. Measurements are performed using Ramsey interferometry and direct optical readout of the nuclear and electron spins. We extract coupling parameters Q (for 14N-V), D, A‖, A⊥, and , and their temperature dependences for both isotopes. The temperature dependences of the nuclear-spin transitions within the spin manifold near room temperature are found to be 0.52(1) ppm/K for 14N-V(|mI = -1⟩ ↔ |mI = +1⟩) and -1.1(1) ppm/K for 15N-V(|mI = -1/2⟩ ↔ |mI = +1/2⟩). An isotopic shift in the zero-field splitting parameter D between 14N-V and 15N-V is measured to be ~ 120 kHz. Residual transverse magnetic fields are observed to shift the nuclear-spin transition frequencies, especially for 15N-V. We have precisely determined the set of parameters relevant for the development of nuclear-spin-based diamond quantum sensors with greatly reduced sensitivity to environmental factors.
Figures
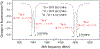
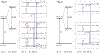



References
-
- Degen CL, Reinhard F, and Cappellaro P, Quantum sensing, Rev. Mod. Phys 89, 035002 (2017).
-
- Ledbetter MP, Jensen K, Fischer R, Jarmola A, and Budker D, Gyroscopes based on nitrogen-vacancy centers in diamond, Phys. Rev. A 86, 052116 (2012).
-
- Ajoy A and Cappellaro P, Stable three-axis nuclear-spin gyroscope in diamond, Phys. Rev. A 86, 062104 (2012).
-
- Maclaurin D, Doherty MW, Hollenberg LCL, and Martin AM, Measurable Quantum Geometric Phase from a Rotating Single Spin, Phys. Rev. Lett 108, 240403 (2012). - PubMed
-
- Kornack TW, Ghosh RK, and Romalis MV, Nuclear Spin Gyroscope Based on an Atomic Comagnetometer, Phys. Rev. Lett 95, 230801 (2005). - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
