Estimation of the mass density of biological matter from refractive index measurements
- PMID: 38718671
- PMCID: PMC11090064
- DOI: 10.1016/j.bpr.2024.100156
Estimation of the mass density of biological matter from refractive index measurements
Abstract
The quantification of physical properties of biological matter gives rise to novel ways of understanding functional mechanisms. One of the basic biophysical properties is the mass density (MD). It affects the dynamics in sub-cellular compartments and plays a major role in defining the opto-acoustical properties of cells and tissues. As such, the MD can be connected to the refractive index (RI) via the well known Lorentz-Lorenz relation, which takes into account the polarizability of matter. However, computing the MD based on RI measurements poses a challenge, as it requires detailed knowledge of the biochemical composition of the sample. Here we propose a methodology on how to account for assumptions about the biochemical composition of the sample and respective RI measurements. To this aim, we employ the Biot mixing rule of RIs alongside the assumption of volume additivity to find an approximate relation of MD and RI. We use Monte-Carlo simulations and Gaussian propagation of uncertainty to obtain approximate analytical solutions for the respective uncertainties of MD and RI. We validate this approach by applying it to a set of well-characterized complex mixtures given by bovine milk and intralipid emulsion and employ it to estimate the MD of living zebrafish (Danio rerio) larvae trunk tissue. Our results illustrate the importance of implementing this methodology not only for MD estimations but for many other related biophysical problems, such as mechanical measurements using Brillouin microscopy and transient optical coherence elastography.
Copyright © 2024 The Author(s). Published by Elsevier Inc. All rights reserved.
Conflict of interest statement
Declaration of interests The authors declare no competing interests.
Figures

 ,
,  ,
,  ,
,  ,
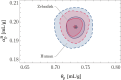
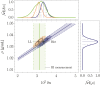
,  ) for , and . The dashed lines indicate the analytical solutions of Eq. 15. (C) Correlative distribution of the MD ρ and the RI contrast (the solid and dashed lines indicate the 68% and 95% confidence contours) with the corresponding normalized marginal probability density distributions and , respectively (the solid line represents the median, the dash-dotted and dashed lines indicate the 68% and 95% CIs), for the exact relative lipid volume fraction (purple) and the relative lipid volume fraction following a truncated normal distribution (cyan; see main text). The MC simulations were performed for a water volume fraction following a truncated normal distribution , and .
) for , and . The dashed lines indicate the analytical solutions of Eq. 15. (C) Correlative distribution of the MD ρ and the RI contrast (the solid and dashed lines indicate the 68% and 95% confidence contours) with the corresponding normalized marginal probability density distributions and , respectively (the solid line represents the median, the dash-dotted and dashed lines indicate the 68% and 95% CIs), for the exact relative lipid volume fraction (purple) and the relative lipid volume fraction following a truncated normal distribution (cyan; see main text). The MC simulations were performed for a water volume fraction following a truncated normal distribution , and .
References
-
- Engler A.J., Sen S., Discher D.E., et al. Matrix Elasticity Directs Stem Cell Lineage Specification. Cell. 2006;126:677. - PubMed
-
- Egan P., Sinko R., et al. Keten S. The role of mechanics in biological and bio-inspired systems. Nat. Commun. 2015;6:7418. - PubMed
-
- Biswas A., Munoz O., Reber S., et al. Conserved nucleocytoplasmic density homeostasis drives cellular organization across eukaryotes. bioRxiv. 2023 doi: 10.1101/2023.09.05.556409. Preprint at. - DOI
MeSH terms
LinkOut - more resources
Full Text Sources
Research Materials

