Mixed selectivity: Cellular computations for complexity

Abstract

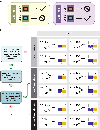
The property of mixed selectivity has been discussed at a computational level and offers a strategy to maximize computational power by adding versatility to the functional role of each neuron. Here, we offer a biologically grounded implementational-level mechanistic explanation for mixed selectivity in neural circuits. We define pure, linear, and nonlinear mixed selectivity and discuss how these response properties can be obtained in simple neural circuits. Neurons that respond to multiple, statistically independent variables display mixed selectivity. If their activity can be expressed as a weighted sum, then they exhibit linear mixed selectivity; otherwise, they exhibit nonlinear mixed selectivity. Neural representations based on diverse nonlinear mixed selectivity are high dimensional; hence, they confer enormous flexibility to a simple downstream readout neural circuit. However, a simple neural circuit cannot possibly encode all possible mixtures of variables simultaneously, as this would require a combinatorially large number of mixed selectivity neurons. Gating mechanisms like oscillations and neuromodulation can solve this problem by dynamically selecting which variables are mixed and transmitted to the readout.

Keywords: brain; circuits; coding; cognition; computations; gating; mixed selectivity; neuromodulation; neuron; oscillations.

Figure 1:. Delineating Pure, Linear Mixed, and Nonlinear Mixed Selectivity using a context dependent Task.

a) In the task, a subject is presented with one of two context signals and subsequently makes a choice from two cues. Rewards are determined based on the initial context. b) A flowchart accompanied by circuits elucidates the neuron response categories: pure, linear mixed, or nonlinearly mixed selectivity. Within each circuit, two initiating neurons are distinctly selective for either the context or the cue, directing their specific signals (I_a and I_b) to a third downstream neuron. Alongside each circuit, diagrams exhibit the neuron’s firing rate in relation to the cumulative input current. The neuron initiates activity when the combined current (here depicted as a histogram) surpasses a certain threshold, leading to a linear increase in the firing rate. If a neuron’s activity is solely representative of a single input, it’s termed ‘purely selective’, exemplified in the top circuits where activation is exclusively due to the cue signal. Neurons that represent a linear combination of the independent inputs, consistently responding to their variable combinations, are termed ‘linear mixed selective’, demonstrated by the middle circuits. Here, the neuron has diminished firing rates for individual signals but is most active when both signals combine. Conversely, ‘nonlinear mixed selective’ neurons, represented in the bottom circuits, cannot be described as a linear sum of inputs. Here, the downstream neuron only becomes active when both the cue and context signals are present simultaneously.

Figure 2:. Changes in the representational geometry due to linear and nonlinear mixed selectivity.

The plots showcase the firing rates of three neurons in response to different combinations of stimuli (S) and contexts (C), both holding two possible values. For simplicity two the firing rates r₁ and r₂ are depicted as being purely selective to either the context or the stimuli. a) Pure Selectivity: Here, r₃’s activity is inversely related to S (r₃=1-S). The three-dimensional plot reveals that, in the activity space, the four combinations of S and C outline a rectangle. Corresponding raster plots below display the firing patterns of these neurons for each S and C combination, revealing distinct activation based on their selectivity. b) Linear Mixed Selectivity: with r₄ responding to a linear combination of the context and stimuli the quadrangle outlined by the four combinations is rotated in this activity space. c) Nonlinear Mixed Selectivity: With r₅ demonstrating nonlinear mixed selectivity, the activity space transforms, with the four points now constituting a 3D tetrahedron.

Figure 3:. Understanding Dimensionality in Neuronal Readouts.

a) Social transmission of food preference is a more ethological variant of the delayed match to sample task, showcasing context-dependent decision making. Initially, a mouse meets a conspecific with a breath scent of an unfamiliar fruit, either a banana (C=0), or a strawberry (C=1). Subsequently, it finds two new fruits – a banana (S=0) and a strawberry (S=1). Informed by the prior interaction, the mouse’s choice is steered by the social transmission of food preference, leaning towards the fruit it detected earlier. b-c) The role of dimensionality in solving complex tasks. b) A downstream neuron receiving activity from r₁, r₂, and r₃ can implement a linear readout to perform simple tasks such as distinguishing between a banana and a strawberry (S=0 vs S=1). c) For more complex tasks such as firing when the context smell matches the stimulus (C=0, S=0 or C=1, S=1), it is not possible for a downstream neuron to implement a linear readout to solve this task. However, a downstream neuron that receives the activity of r₁, r₂ and r₅ as input can easily perform a linear readout due to the higher dimensionality achieved by the nonlinear selectivity of r₅. Created with BioRender.com.

Figure 4:. Why we cannot mix everything together.

a) Number of neurons that are needed as a function of the number of variables that should be mixed for each task, when the number of tasks 1/F increases (where F is the fraction of all the variables that have to be mixed per task). The red curve is for a relatively simple task, with 10 binary variables, and the blue curve is for a more complex task with 20 variables. b) The basic principle of dynamic gating. Here, we have a simple three-layer feedforward neural network that can compute the Exclusive-OR function of the input. With a three-unit hidden layer the network achieves maximum dimensionality with two inputs and can easily compute the Exclusive-OR. With four input neurons as we have in this example, we need to either increase the number of hidden units, or gate half of the input using a context signal such as is shown here. c) Dynamic mixing using oscillations. One way how this gating can be implemented biologically is through some of the input and downstream neurons to receive the same oscillatory input. In context 1 when the oscillatory input to the neurons coding for feature 1 and 2 is high, it will be easier for the neurons to spike, thus making it easier for the downstream neuron to integrate their signals and fire. Similarly, if that oscillatory input is low it will be harder for these neurons to spike. d) Dynamic gating using neuromodulation. Here the context signal takes the form of a neuromodulatory signal that makes it easier for neurons with the correct receptors to become excited, thus facilitating the integration of the firing of neurons 1 and 2 by the downstream neuron in the bottom picture.