Topological defects in multi-layered swarming bacteria

Abstract

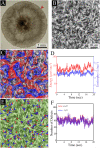
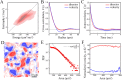
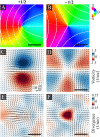
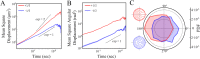
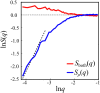
Topological defects, which are singular points in a director field, play a major role in shaping active systems. Here, we experimentally study topological defects and the flow patterns around them, that are formed during the highly rapid dynamics of swarming bacteria. The results are compared to the predictions of two-dimensional active nematics. We show that, even though some of the assumptions underlying the theory do not hold, the swarm dynamics is in agreement with two-dimensional nematic theory. In particular, we look into the multi-layered structure of the swarm, which is an important feature of real, natural colonies, and find a strong coupling between layers. Our results suggest that the defect-charge density is hyperuniform, i.e., that long range density-fluctuations are suppressed.

Fig. 1. B. subtilis swarming. (A) A top-view macroscopic image of a B. subtilis colony; the arrow indicates the region of interest shown in B. (B) A top-view microscopic image of fluorescently labeled B. subtilis swarming cells taken with a 40× objective. The field of view is 150 μm × 150 μm. (C) Velocity field (in the background of the cells) calculated using an optical flow method, demonstrating chaotic collective swirling motion. Blue and red colors indicate clockwise and counterclockwise rotating regions. (D) Time evolution of enstrophy Ω (blue) and kinetic energy per unit mass E (red). (E) The nematic director field extracted from (B) with positive (red) and negative (blue) locations and orientations of half-integer defects. (F) Time evolution of the observed number of +1/2 (red) and −1/2 (blue) defects.

Fig. 2. Statistical analysis of the director and velocity fields. (A) Enstrophy Ω vs. kinetic energy E for each timepoint throughout the entire experiment, presented as a density map (B) and (C) cross-correlation and autocorrelation functions of the director (red) and velocity (blue) fields. (D) Okubo–Weiss field thresholded to negative values, Q < 0. Blue and red domains denote clockwise and counterclockwise rotating regions. (E) Log-linear representation of the vortex area probability density distribution. The dotted line shows an exponential fit. (F) The mean vorticity per vortex is normalized by the square root of enstrophy ω/Ω^1/2 as a function of the vortex area. Blue and red curves represent clockwise and counterclockwise rotating vortices.

Fig. 3. Ensemble average of director and flow fields near +1/2 and −1/2 nematic defects, as obtained from experiments, centered and aligned. (A) and (B) Director fields depicting +1/2 and −1/2 defects. The color maps and overlaid white lines show the ensemble average of the director orientation, varying from −π to π. (C) and (D) Average velocity fields. Colors indicate the vorticity (C) and (D) and divergence (E) and (F) for +1/2 (left) and −1/2 (right) defects. The superimposed black arrows indicate the direction of the velocity field. The magnitude of the velocity field is indicated by the black arrow, corresponding to a value of 10 μm s⁻¹. The scale bar is 10 μm.

Fig. 4. Statistical analysis of +1/2 and −1/2 defect trajectories. (A) and (B) Averaged mean square displacement (MSD) of defect position (A) and direction (B) for +1/2 (red) and −1/2 (blue) defects on a log–log scale. The dashed lines are guides to the eye with slopes 1 (diffusive) and 2 (ballistic). (C) Probability density distribution of the relative angle between the velocity vector and the defect orientation. Sketches illustrate the nematic orientation around +1/2 (red) and −1/2 (blue) defects.

Fig. 5. Defect structure factors. Red curve: the structure factor of the overall defect density, S_both(q), shows long range attraction. Blue curve: the structure factor for the defect charge, S_ρ(q), shows reduction at small q values, suggesting suppression of large-scale fluctuations. The dashed line is a guide to the eye with slope 2, the theoretical prediction for ionic solutions at equilibrium. The vanishing of S_ρ(q) in the limit q → 0 is the hallmark of hyperuniformity.

Fig. 6. Comparison between layers—director and velocity fields. (A) and (B) Simultaneous snapshots showing the director and velocity fields at the bottom layer near the substrate (h1) and at the top layer (h2) of the swarm. (C) and (D) The probability density distribution of the difference in directions of the nematic director (C, red) and velocity (D, blue) fields between the bottom and top layers.

Fig. 7. Comparison between layers—defects. (A) Simultaneous snapshots show defects at the bottom layer near the substrate (h1) and the top layer (h2). Inset (A) zoom-in illustrating top-bottom defect pairs of the same sign. The color code in the inset indicates to which layer the defects belong. (B) The displacement probability between pairs of defects (+1/2, +1/2 red and −1/2, −1/2 blue), is normalized by randomly distributed defects. A probability of 1 corresponds to an uncorrelated distribution. The inset shows a uniform probability density function (PDF) of displacement direction relative to the defect orientation. (C) PDF of the phase φ between defect pairs (φ^+1/2 red and φ^−1/2 blue). The phase definition is illustrated in the sketch at the upper right. (D) Standard deviation of φ as a function of their displacement (φ^+1/2 red and φ^−1/2 blue).