A predictor-informed multi-subject bayesian approach for dynamic functional connectivity

Abstract

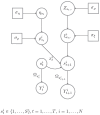
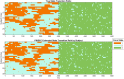
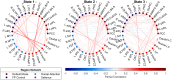
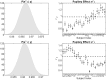
Dynamic functional connectivity investigates how the interactions among brain regions vary over the course of an fMRI experiment. Such transitions between different individual connectivity states can be modulated by changes in underlying physiological mechanisms that drive functional network dynamics, e.g., changes in attention or cognitive effort. In this paper, we develop a multi-subject Bayesian framework where the estimation of dynamic functional networks is informed by time-varying exogenous physiological covariates that are simultaneously recorded in each subject during the fMRI experiment. More specifically, we consider a dynamic Gaussian graphical model approach where a non-homogeneous hidden Markov model is employed to classify the fMRI time series into latent neurological states. We assume the state-transition probabilities to vary over time and across subjects as a function of the underlying covariates, allowing for the estimation of recurrent connectivity patterns and the sharing of networks among the subjects. We further assume sparsity in the network structures via shrinkage priors, and achieve edge selection in the estimated graph structures by introducing a multi-comparison procedure for shrinkage-based inferences with Bayesian false discovery rate control. We evaluate the performances of our method vs alternative approaches on synthetic data. We apply our modeling framework on a resting-state experiment where fMRI data have been collected concurrently with pupillometry measurements, as a proxy of cognitive processing, and assess the heterogeneity of the effects of changes in pupil dilation on the subjects' propensity to change connectivity states. The heterogeneity of state occupancy across subjects provides an understanding of the relationship between increased pupil dilation and transitions toward different cognitive states.

Fig 1. Graphical representation of the proposed PIBDFC.

The data $Y_t^i$ are emissions from a distribution that is parameterized by a precision matrix ${\Omega }_{s_t^i}$, which encodes the FC and is determined by the state active at time t: $s_t^i\in \{1,\dots ,S$, t = 1, …, T, i = 1, …, N. The probabilities of transitions from $s_t^i$ to $s_{t+1}^i$ are given by the $(s_t^i,s_{t+1}^i)$ entry of the S × S matrix $Q_{·,·,t}^i$. This entry is modeled according to Eq 3.

Fig 2. Example estimation of state related partial correlation matrices on simulated data.

Top: The true partial correlation matrices for each state responsible for generating the simulation data in the Simulation Study 1. Bottom: The estimated partial correlation matrix from the proposed PIBDFC from a single repetition of the simulation. Each estimated partial correlation is the posterior mean of their respective distributions. Cells are set to 0 in post-hoc MCMC by controlling the BFDR at the 0.2 level. See Sections 2 and 3 for details.

Fig 3. Edge detection performance by PIBDFC, BDFC, and Tapered SW.

True Positive Rate, True Negative Rate, F1 Score, and state accuracy metrics for the PIBDFC, BDFC, and Tapered SW approaches over different settings of the correlation structure. Along each horizontal axis is the average strength of the non-zero partial correlations for each state, corresponding to different levels of signal strength.

Fig 4. Example estimation of state transitions on simulated data.

Top: The true state transition path for each subject (vertical axis) across each time point (horizontal axis). The color in each cell identifies which precision matrix in Fig 2 generated the simulated the data for each subject-time point pairs. Bottom: The maximum a posteriori estimated state trajectories from PIBDFC.

Fig 5. Example estimation of state changepoints on simulated data.

Estimation of the connectivity change points in a representative subject. The horizontal axis indicates the time points while the vertical axis reports the posterior probability $P(s_t^1\ne s_{t-1}^1|Y_{1:T}^i)$. The posterior probabilities of a change point are in red, whereas the black spikes represent the true change points for the subject. We also display a horizontal dotted line at 0.95 to reflect the informal rule of declaring a change-point if $P(s_t^1\ne s_{t-1}^1|Y_{1:T}^i)>0.95$.

Fig 6. Real Data Analysis: The estimated connectivity networks for the ROIs.

Nodes represent ROIs and the edges denote the partial correlations between the connected nodes. The edge colors correspond to the directionality of the partial correlations and the width corresponds to the magnitude. Node colors identify clusters of regions into a priori defined networks. See Section 4 and S1 Table in the S1 File.

Fig 7. Real Data Analysis: Estimated states’ transition path for each subject.

The horizontal axis indicates the TR with vertical dotted lines indicating portions where the subject raises their arm. Subject sequences are aligned so that the first 525 time points show sequences from the sham condition and the time points 526–1050 show sequences from the active condition. The vertical axis displays the subject indices, ordered by similarity in state trajectory according to a hierarchical clustering (based on the Euclidean distance) of their MAP transition behavior.

Fig 8. Estimated effects of pupil dilation on state transition probability.

Real Data Analysis: The posterior distribution of the group effect of pupillary dilation e^η (left), and individual effects of pupillary dilation e^ρ. Rows indicate the propensity for transitioning into states 2 and 3 respectively. For the individual effects, subjects are identically ordered as in Fig 7. The horizontal dotted line is the posterior mean for the group-level effects, η₂ = 0.687 and η₃ = 0.651 respectively.