Interpretable online network dictionary learning for inferring long-range chromatin interactions
- PMID: 38753877
- PMCID: PMC11135774
- DOI: 10.1371/journal.pcbi.1012095
Interpretable online network dictionary learning for inferring long-range chromatin interactions
Abstract
Dictionary learning (DL), implemented via matrix factorization (MF), is commonly used in computational biology to tackle ubiquitous clustering problems. The method is favored due to its conceptual simplicity and relatively low computational complexity. However, DL algorithms produce results that lack interpretability in terms of real biological data. Additionally, they are not optimized for graph-structured data and hence often fail to handle them in a scalable manner. In order to address these limitations, we propose a novel DL algorithm called online convex network dictionary learning (online cvxNDL). Unlike classical DL algorithms, online cvxNDL is implemented via MF and designed to handle extremely large datasets by virtue of its online nature. Importantly, it enables the interpretation of dictionary elements, which serve as cluster representatives, through convex combinations of real measurements. Moreover, the algorithm can be applied to data with a network structure by incorporating specialized subnetwork sampling techniques. To demonstrate the utility of our approach, we apply cvxNDL on 3D-genome RNAPII ChIA-Drop data with the goal of identifying important long-range interaction patterns (long-range dictionary elements). ChIA-Drop probes higher-order interactions, and produces data in the form of hypergraphs whose nodes represent genomic fragments. The hyperedges represent observed physical contacts. Our hypergraph model analysis has the objective of creating an interpretable dictionary of long-range interaction patterns that accurately represent global chromatin physical contact maps. Through the use of dictionary information, one can also associate the contact maps with RNA transcripts and infer cellular functions. To accomplish the task at hand, we focus on RNAPII-enriched ChIA-Drop data from Drosophila Melanogaster S2 cell lines. Our results offer two key insights. First, we demonstrate that online cvxNDL retains the accuracy of classical DL (MF) methods while simultaneously ensuring unique interpretability and scalability. Second, we identify distinct collections of proximal and distal interaction patterns involving chromatin elements shared by related processes across different chromosomes, as well as patterns unique to specific chromosomes. To associate the dictionary elements with biological properties of the corresponding chromatin regions, we employ Gene Ontology (GO) enrichment analysis and perform multiple RNA coexpression studies.
Copyright: © 2024 Rana et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures





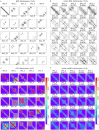


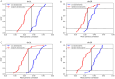
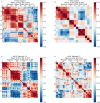
References
-
- Cichocki A, Lee H, Kim YD, Choi S. Non-negative matrix factorization with α-divergence. Pattern Recognition Letters. 2008;29(9):1433–1440. doi: 10.1016/j.patrec.2008.02.016 - DOI
-
- Ye M, Qian Y, Zhou J. Multitask sparse nonnegative matrix factorization for joint spectral–spatial hyperspectral imagery denoising. IEEE Transactions on Geoscience and Remote Sensing. 2014;53(5):2621–2639. doi: 10.1109/TGRS.2014.2363101 - DOI
-
- Lu H, Sang X, Zhao Q, Lu J. Community detection algorithm based on nonnegative matrix factorization and pairwise constraints. Physica A: Statistical Mechanics and its Applications. 2020;545:123491. doi: 10.1016/j.physa.2019.123491 - DOI
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

