Transcription factors ERα and Sox2 have differing multiphasic DNA- and RNA-binding mechanisms
- PMID: 38760076
- PMCID: PMC11251522
- DOI: 10.1261/rna.080027.124
Transcription factors ERα and Sox2 have differing multiphasic DNA- and RNA-binding mechanisms
Abstract
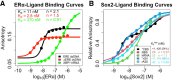
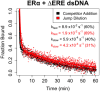
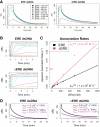
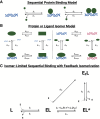
Many transcription factors (TFs) have been shown to bind RNA, leading to open questions regarding the mechanism(s) of this RNA binding and its role in regulating TF activities. Here, we use biophysical assays to interrogate the k on, k off, and K d for DNA and RNA binding of two model human TFs, ERα and Sox2. Unexpectedly, we found that both proteins exhibit multiphasic nucleic acid-binding kinetics. We propose that Sox2 RNA and DNA multiphasic binding kinetics can be explained by a conventional model for sequential Sox2 monomer association and dissociation. In contrast, ERα nucleic acid binding exhibited biphasic dissociation paired with novel triphasic association behavior, in which two apparent binding transitions are separated by a 10-20 min "lag" phase depending on protein concentration. We considered several conventional models for the observed kinetic behavior, none of which adequately explained all the ERα nucleic acid-binding data. Instead, simulations with a model incorporating sequential ERα monomer association, ERα nucleic acid complex isomerization, and product "feedback" on isomerization rate recapitulated the general kinetic trends for both ERα DNA and RNA binding. Collectively, our findings reveal that Sox2 and ERα bind RNA and DNA with previously unappreciated multiphasic binding kinetics, and that their reaction mechanisms differ with ERα binding nucleic acids via a novel reaction mechanism.
Keywords: DNA; RNA; kinetics; transcription factor.
© 2024 Hemphill et al.; Published by Cold Spring Harbor Laboratory Press for the RNA Society.
Figures






Update of
-
Transcription factors ERα and Sox2 have differing multiphasic DNA and RNA binding mechanisms.bioRxiv [Preprint]. 2024 Mar 19:2024.03.18.585577. doi: 10.1101/2024.03.18.585577. bioRxiv. 2024. Update in: RNA. 2024 Jul 16;30(8):1089-1105. doi: 10.1261/rna.080027.124. PMID: 38562825 Free PMC article. Updated. Preprint.
References
-
- Chassaing N, Causse A, Vigouroux A, Delahaye A, Alessandri J-L, Boespflug-Tanguy O, Boute-Benejean O, Dollfus H, Duban-Bedu B, Gilbert-Dussardier B, et al. 2014. Molecular findings and clinical data in a cohort of 150 patients with anophthalmia/microphthalmia. Clin Genet 86: 326–334. 10.1111/cge.12275 - DOI - PubMed
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
