Bayesian Estimation of Muscle Mechanisms and Therapeutic Targets Using Variational Autoencoders

Abstract

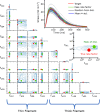
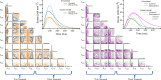
Cardiomyopathies, often caused by mutations in genes encoding muscle proteins, are traditionally treated by phenotyping hearts and addressing symptoms post irreversible damage. With advancements in genotyping, early diagnosis is now possible, potentially introducing earlier treatment. However, the intricate structure of muscle and its myriad proteins make treatment predictions challenging. Here we approach the problem of estimating therapeutic targets for a mutation in mouse muscle using a spatially explicit half sarcomere muscle model. We selected 9 rate parameters in our model linked to both small molecules and cardiomyopathy-causing mutations. We then randomly varied these rate parameters and simulated an isometric twitch for each combination to generate a large training dataset. We used this dataset to train a Conditional Variational Autoencoder (CVAE), a technique used in Bayesian parameter estimation. Given simulated or experimental isometric twitches, this machine learning model is able to then predict the set of rate parameters which are most likely to yield that result. We then predict the set of rate parameters associated with twitches from control mice with the cardiac Troponin C (cTnC) I61Q variant and control twitches treated with the myosin activator Danicamtiv, as well as model parameters that recover the abnormal I61Q cTnC twitches.

Figure 1:

Left: 3D rendering of a sarcomere’s lattice showing the thick (red) and thin filaments (blue) as well as a superimposed spring network to give a sense of the model’s geometry. Following the geometry specified in (7) we model the filaments as a network of springs for the thick and thin filaments, with crossbridges, each consisting of a torsional and linear spring. Right: The rate transition diagram for the thick and thin filaments, indicating the four thin filament rates (labeled $r_t$) and the six myosin motor rates (labeled $r_x$), as well as a table indicating the key biological elements. Crossbridges are modeled as a torsional and linear spring.

Figure 2:

The forward and backward rate functions for the myosin binding and power stroke cycling are plotted as a function of the axial separation between a crossbridge and a binding site. The rates $r_{x,16}$ and $r_{x,61}$ given for a pCa of 4. Not shown are the thick filaments rates $r_{x,15}$ and $r_{x,54}$ as well as the thin filament rate $r_{t,14}$ which are all 0.

Figure 3:

The encoding and decoding networks $Q_1,R_1$, and $R_2$ are each composed of the same shared deep convolutional layers. The loss function −L+KL is composed of the log probability of the true rate at for the estimated probability distribution function (L), and the Kullback-Liebler divergence (KL) between the probability distributions from the $Q_1$ and $R_1$ networks (KL). ${\mathrm{\Phi }}_{Q_1},{\mathrm{\Phi }}_{R_1}$, and ${\mathrm{\Phi }}_{R_2}$ are the probability distributions generated by the separate networks, and $\mu ,\mathrm{\Sigma }$, and $w$ are the means, variances, and weights of the components of each of the Gaussian Mixture distributions. The points $z_{Q_1}$ and $z_{R_1}$ are random points drawn from their respective distributions over the latent space, and $r_{R_2}$ is a random rate drawn from its distribution. This architecture follows that found in (8).

Figure 4:

The Probability-Probability plot shows how well our estimated probability distribution describes the actual probability distribution across our validation dataset. The x-axis shows the estimated probability the rate is contained in a certain volume of the rate space, and the y-axis indicates the actual fraction of times the rate was contained in that volume. For an ideal predictor, the true parameter should be in the X% credible region X% of the time, indicated by the black dashed line. Values above the diagonal indicate under-confidence, and values below indicate over-confidence.

Figure 5:

The 2-D joint probability distributions for the 9 rates we chose to vary in our simulations are shown as contour plots that indicate the probability density over the rate space. The 1-D marginalized probability distribution of every rate factor is plotted along the diagonal. In each joint probability distribution, solid red dots indicate the true rate factor which the target twitch had been generated with. The target twitch, drawn from the simulated validation subset, is shown in the upper right in red. A second inset shows a blowup of the joint probability distribution for $r_{t,12}$ and $r_{t,34}$, with the true rate factor indicated as a solid red dot. We also show the peak of the distribution as a solid green dot, and the resulting twitch simulated with that rate factor combination is shown in the upper right in green. Also shown are 20 twitches (black) and their mean ± standard deviation (blue) which were simulated with rate factors drawn randomly from the distribution. The rate factors are multiplied by the base rates, plotted in Fig. 2. Note that the rate factors are plotted on a log scale.

Figure 6:

Here we show the experimental isometric twitch stress for the different conditions used in the CVAE. First, we show mouse cardiac trabeculae from control (blue) and mice with the I61Q cTnC variant (orange). We also show control trabecula (green) and trabecula treated with the myosin activator Danicamtiv (pink), previously published in (12). We show the control datasets taken contemporaneously for both I61Q cTnC and the Danicamtiv, since a different experimental apparatus and protocol was used. For each group, the overall average (dashed black line) is shown along with the 95% confidence of the mean intervals (shaded region). The I61Q cTnC groups consisted of 8 individuals, while the Danicamtiv groups consisted of 4 individuals.

Figure 7:

As in Fig. 5, we show the 2-D joint probability distributions as contour plots that indicate the probability density over the rate factor space. Here, however, our target twitches were the mean experimental data shown in Fig. 6 rather than simulated data, and dots indicate the peak of the probability distribution, i.e. the most probable value. In the left panel, we show the experimental twitches as well as the twitch simulated using rate parameters corresponding to the peak of the respective distribution. In the right panel, we show the same using data previously published in (12). As before, the rate factors are multiplied by the base rates, plotted in Fig. 2. Note that the rate factors are plotted on a log scale.

Figure 8:

Left) Isometric twitch stress is plotted against time. Dotted lines indicate the experimental data, and solid lines indicate simulated data. The blue and and orange simulations are performed with the most probable rates identi from the distributions shown in figure 7. The ‘hybrid’ twitch (green) combines rates from those two inferences: the $r_{t,12}$ and $r_{t,14}$ rates from I61Q, and the control rates for the rest. Middle) Starting with the ‘hybrid’ twitch and using the Control twitch as a target, we trained a separate CVAE on only the thick filament rates in order to estimate an ‘intervention’ in the thick filament, i.e. changes we could make which would restore function. For this set of simulations we centered the training set around the ‘Hybrid’ rate factors, represented by green dots.Here, we show the resulting distribution over the thick filament rates using the control twitch as a target. As in Fig. 7, solid red dots indicate the most probable rate factor, and rate factors are plotted on a log scale. Right) We show the resulting simulated twitch corresponding to the peak of the distribution, which is our best estimate for a thick filament intervention. In short, we started with the control twitch (blue), reduced $r_{t,12}$ and $r_{t,14}$ to estimate an I61Q twitch (green), then estimate what change would be necessary to restore function, i.e. give a twitch most similar to the control (red).