Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Comparative Study
. 2024 Jun 20;31(7):1514-1521.
doi: 10.1093/jamia/ocae109.

Comparing penalization methods for linear models on large observational health data

Egill A Fridgeirsson  1 , Ross Williams  1 , Peter Rijnbeek  1 , Marc A Suchard  2   3 , Jenna M Reps  1   4
Affiliations
Comparative Study

Comparing penalization methods for linear models on large observational health data

Egill A Fridgeirsson et al. J Am Med Inform Assoc. .

Abstract

Objective: This study evaluates regularization variants in logistic regression (L1, L2, ElasticNet, Adaptive L1, Adaptive ElasticNet, Broken adaptive ridge [BAR], and Iterative hard thresholding [IHT]) for discrimination and calibration performance, focusing on both internal and external validation.

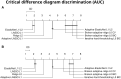
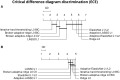
Materials and methods: We use data from 5 US claims and electronic health record databases and develop models for various outcomes in a major depressive disorder patient population. We externally validate all models in the other databases. We use a train-test split of 75%/25% and evaluate performance with discrimination and calibration. Statistical analysis for difference in performance uses Friedman's test and critical difference diagrams.

Results: Of the 840 models we develop, L1 and ElasticNet emerge as superior in both internal and external discrimination, with a notable AUC difference. BAR and IHT show the best internal calibration, without a clear external calibration leader. ElasticNet typically has larger model sizes than L1. Methods like IHT and BAR, while slightly less discriminative, significantly reduce model complexity.

Conclusion: L1 and ElasticNet offer the best discriminative performance in logistic regression for healthcare predictions, maintaining robustness across validations. For simpler, more interpretable models, L0-based methods (IHT and BAR) are advantageous, providing greater parsimony and calibration with fewer features. This study aids in selecting suitable regularization techniques for healthcare prediction models, balancing performance, complexity, and interpretability.

Keywords: calibration; discrimination; electronic health records; logistic regression; regularization.

PubMed Disclaimer

Conflict of interest statement

E.A.F. and P.R. work for a research group who received unconditional research grants from Boehringer-Ingelheim, GSK, Janssen Research & Development, Novartis, Pfizer, Yamanouchi, Servier. None of these grants result in a conflict of interest to the content of this paper. J.M.R. is an employee of Janssen R&D and shareholder of JNJ. M.A.S. receives contracts and grants from the US National Institutes of Health, the US Food & Drug Administration and Janssen Research & Development, all outside the scope of this work.

Figures

Figure 1.
Figure 1.
A patient level prediction problem. Conditions, drugs, procedures, and observations from an observation window prior to an index date are used to predict the outcome during a time-at-risk after index. Reproduced from John et al with permission from BMC Medical Research Methodology.
Figure 2.
Figure 2.
(A) Critical difference diagram of the developed models ranked using internal AUC. (B) Critical difference diagram ranked using external AUC. The critical difference (CD) line indicates how big of a difference is needed to be significantly different. Solid lines connect algorithms with no significant difference between them. Abbreviations: BIC = Bayesian information criteria, CV = cross validation.
Figure 3.
Figure 3.
Expected calibration error (ECE) ranked according to (A) internal and (B) external performance. Abbreviations: CD = critical difference, BIC = Bayesian information criteria, CV = cross validation.
Figure 4.
Figure 4.
Distributions of model sizes for the 840 developed models. The vertical line and red number represent the median model size. Abbreviations: BIC = Bayesian information criteria, CV = cross validation.
See this image and copyright information in PMC

References

    1. Yang C, Kors JA, Ioannou S, et al. Trends in the conduct and reporting of clinical prediction model development and validation: a systematic review. J Am Med Inform Assoc. 2022;29(5):983-989. - PMC - PubMed
    1. Tibshirani R. Regression shrinkage and selection via the LASSO. J R Stat Soc B. 1996;58(1):267-288.
    1. Khalid S, Yang C, Blacketer C, et al. A standardized analytics pipeline for reliable and rapid development and validation of prediction models using observational health data. Comput Methods Programs Biomed. 2021;211:106394. - PMC - PubMed
    1. Siontis GCM, Tzoulaki I, Castaldi PJ, et al. External validation of new risk prediction models is infrequent and reveals worse prognostic discrimination. J Clin Epidemiol. 2015;68(1):25-34. - PubMed
    1. Suchard MA, Simpson SE, Zorych I, et al. Massive parallelization of serial inference algorithms for a complex generalized linear model. ACM Trans Model Comput Simul. 2013;23(1):1. - PMC - PubMed

Publication types