Learning capabilities to resolve tilt-translation ambiguity in goldfish

Abstract

Introduction: Spatial orientation refers to the perception of relative location and self-motion in space. The accurate formation of spatial orientation is essential for animals to survive and interact safely with their environment. The formation of spatial orientation involves the integration of sensory inputs from the vestibular, visual, and proprioceptive systems. Vestibular organs function as specialized head motion sensors, providing information regarding angular velocity and linear acceleration via the semicircular canals and otoliths, respectively. However, because forces arising from the linear acceleration (translation) and inclination relative to the gravitational axis (tilt) are equivalent, they are indistinguishable by accelerometers, including otoliths. This is commonly referred to as the tilt - translation ambiguity, which can occasionally lead to the misinterpretation of translation as a tilt. The major theoretical frameworks addressing this issue have proposed that the interpretation of tilt versus translation may be contingent on an animal's previous experiences of motion. However, empirical confirmation of this hypothesis is lacking.

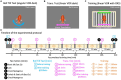
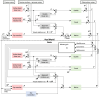
Methods: In this study, we conducted a behavioral experiment using goldfish to investigate how an animal's motion experience influences its interpretation of tilt vs. translation. We examined a reflexive eye movement called the vestibulo-ocular reflex (VOR), which compensatory-rotates the eyes in response to head motion and is known to reflect an animal's three-dimensional head motion estimate.

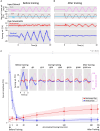
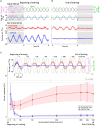
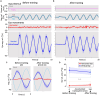
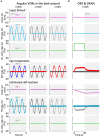
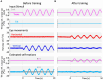
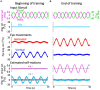
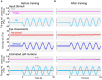
Results: We demonstrated that the VORs of naïve goldfish do not differentiate between translation and tilt at 0.5 Hz. However, following prolonged visual-translation training, which provided appropriate visual stimulation in conjunction with translational head motion, the VORs were capable of distinguishing between the two types of head motion within 3 h. These results were replicated using the Kalman filter model of spatial orientation, which incorporated the variable variance of process noise corresponding to the accumulated motion experience.

Discussion: Based on these experimental and computational findings, we discuss the neural mechanism underlying the resolution of tilt-translation ambiguity within a context analogous to, yet distinct from, previous cross-axis VOR adaptations.

Keywords: Kalman filter model; adaptive learning ability; gravito-inertial axis; somatogravic illusion; spatial orientation; state space model; translation ambiguity; vestibulo-ocular reflex.

Figure 1

(A) Definition of 3D axes in the animals’ head coordination. Positive directions are indicated by arrow heads for both linear and rotational motion. To clarify, yaw and roll-tilt rotations are those around z and x-axis, respectively, which typically induce horizontal and vertical VOR, respectively. Positive directions of yaw (horizontal) and roll (vertical) rotations are clockwise, i.e., rightward in both eyes and downward in the right eye, respectively. (B–D) Experimental setup. (B) Rear view of the system (left) and its configuration diagram (right). The aquarium is removed in this view. Note, visual stimulus and linear translation were not given during actual roll-tilt test paradigm. (C) Top view. Horizontal eye camera is removed in this view. (D) Left side view.

Figure 2

Experiment paradigm. Panels (A–C) are graphical explanations of the roll-tilt test (angular VOR in the dark), translation test (linear VOR in the dark), and training (linear VOR along with OKS), respectively. (D) Schematic overview of the timeline of the experimental protocol. The times in the titles of each paradigm of translation test and training are the accumulated times of training experienced up to that point, which differs from the overall elapsed time because of the test segments inserted before and during training.

Figure 3

Horizontal and vertical VOR in response to interaural translational head acceleration in the dark (translation test) before, during, and after visual-translation training. (A,B) Horizontal (second panels from the bottom, red) and vertical (bottom panels, blue) eye velocities, around the z- and x-axes respectively, averaged over all animals (n = 12) during translational acceleration stimulation in the dark before (A) and after (B) training. Red and blue shadows indicate plus or minus one standard deviation. The top panels show linear velocity along the y-axis converted from the acceleration stimulation (see section 2). The second panels from the top show tilt (rotation around the y-axis) angular velocity, which is 0 during this stimulation and GIA angular velocity calculated from the translational acceleration, both around the x-axis. (C) Inset illustrating the horizontal (red) and vertical (blue) eye velocity traces averaged over stimulus cycles (magenta). The angular velocity traces around different axes (horizontal eye velocity around the z-axis and vertical eye velocity around the x-axis) and linear velocity along the y-axis traces are depicted in the same figures. Below the insets, changes in the mean amplitudes of horizontal and vertical VORs (learning curves) are plotted. Red and blue shadows indicate plus or minus one standard deviation. The increase in mean (±SD) amplitude of horizontal eye velocity and the decrease in mean amplitude of vertical eye velocity before and after training are significant (0.3 ± 0.6 vs. 3.4 ± 1.1 °/s, p < 0.001 for horizontal eye velocity; 12.5 ± 4.1 vs. 0.7 ± 0.4 °/s, p < 0.001 for vertical eye velocity).

Figure 4

Horizontal and vertical VORs in response to interaural translational head acceleration along with OKS (training) during visual-translation training. (A,B) Horizontal (second panels from the bottom, red) and vertical (bottom panels, blue) eye velocities around the z- and x-axes, respectively, averaged over all animals (n = 12) during translational acceleration stimulation along with OKS at the beginning (A) and end (B) of the training. Red and blue shadows indicate plus or minus one standard deviation. The top panels show linear velocity along the y-axis converted from the acceleration stimulation (see section 2), and OKS velocity represented as an angular velocity around the z-axis. The second panels from the top show tilt angular velocity, which is 0 during this stimulation and GIA angular velocity calculated from the translational acceleration, both around the x-axis. (C) Inset illustrating horizontal (red) and vertical (blue) eye velocity traces averaged over stimulus cycles (magenta). The angular velocity traces around different axes (horizontal eye velocity and visual stimulus velocity both around the z-axis, vertical eye velocity around the x-axis) and linear velocity along the y-axis traces are depicted in the same figures. Eye velocities and visual stimulus velocity are depicted in different scales. Below the insets, changes in the mean amplitudes of horizontal and vertical VORs (learning curves) are plotted. Red and blue shadow indicate plus or minus one standard deviation. The increase in mean (±SD) amplitude of horizontal eye velocity and the decrease in mean amplitude of vertical eye velocity between the beginning and end of the training are significant (3.1 ± 1.4 vs. 5.6 ± 2.1 °/s, p = 0.004 for horizontal eye velocity; 5.6 ± 2.3 vs. 0.4 ± 0.3 °/s, p < 0.001 for vertical eye velocity).

Figure 5

Horizontal and vertical VOR in response to roll-tilt head rotation in the dark (roll-tilt test) before, and after visual-translation training. (A,B) Horizontal (second panels from the bottom, red) and vertical (the bottom panels, blue) eye velocities around the z- and x-axes respectively, averaged over all animals (n = 12) during roll-tilt stimulation in the dark before (A) and after (B) training. Red and blue shadows indicate plus or minus one standard deviation. The top panels show linear velocity along the y-axis, which is 0 during this stimulation. The second panels from the top show tilt angular velocity and GIA angular velocity both around the x-axis. (C) Horizontal (red) and vertical (blue) eye velocity traces averaged over stimulus cycles (cyan). Angular velocity traces around different axes (horizontal eye velocity around the z-axis, vertical eye velocity and tilt angular velocity both around the x-axis) are depicted in the same figures. (D) Changes in the mean amplitudes of horizontal and vertical VORs (learning curves). Red and blue shadows indicate plus or minus one standard deviation. Both horizontal and vertical eye velocities show no significant differences between before and after training (0.6 ± 0.6 vs. 1.3 ± 2.0 °/s, p = 0.157 for horizontal eye velocity; 29.1 ± 5.4 vs. 25.4 ± 4.7 °/s, p = 0.060 for vertical eye velocity).

Figure 6

Modified Kalman filter model, where each variable and coefficient are defined in Table 1. The eye motor model, retina model, apparent rotation velocity model, and eye controller were added to the Kalman filter model in Laurens and Angelaki (18) to explain our results of VOR. The apparent rotational velocity model outputs the visual rotational velocity around the head caused by linear acceleration, which is used to linear VOR in the eye controller [Equation (–3)]. To assist in the interpretation of our experiments, particularly with the interpretation of eye movements, passive motion, and process noise, we have also described a world system outside the brain that was not specified in the Kalman filter model by Laurens and Angelaki.

Figure 7

Results of the modified Kalman filter model simulation for model validation. (A) Simulation results of angular VORs around the x-, y-, and z-axes. (B) Simulation results of OKAN around the z-axis. In panels (A,B), the top three rows represent input stimuli (vestibular or visual), the fourth row from the top depicts eye movements, and the bottom three rows show internally estimated self-motions corresponding to their respective input stimuli. The colors “x,” “y,” and “z” in the inset of the leftmost column indicate the directions (rotation around the x-, y-, and z-axes, or translation along the x-, y-, and z-axes). All traces display the average results of the 12 simulation runs. Traces representing minimal values overlap at the baseline and are not all visible.

Figure 8

Results of our modified Kalman filter model simulation in response to interaural translational head acceleration in the dark. In the Kalman filter model, the process noise + passive stimuli standard deviation of interaural linear acceleration was set to a small value (0.001 G) at panel (A) and a large value (0.180 G) at panel (B), to reproduce the translation test paradigms before and after training. The top two rows show input stimuli, with linear velocity stimulation along the y-axis (magenta) and tilt angular velocity around the x-axis (cyan). Tilt angular velocity around the x-axis is 0 during this stimulation. The third and fourth rows from the top show the simulation results of horizontal eye velocity around the z-axis (red) and vertical eye velocity around the x-axis (blue). The bottom two rows show the simulation results of linear velocity along the x-, y-, and z-axes (dark gray, dark magenta, and light gray, respectively) and angular velocity around the x-, y-, and z-axes (dark cyan, dark gray, and light gray, respectively), estimated by the Kalman filter. Eye movements and estimated self-motions traces show the average traces of the 12 simulation runs.

Figure 9

Results of our modified Kalman filter model simulation in response to interaural translational head acceleration along with OKS. In the Kalman filter model, the process noise + passive stimuli standard deviation of interaural linear acceleration was set to a small value (0.001 G) at (A) and a large value (0.180 G) at (B) to reproduce training paradigms at the beginning and end of the training. The top two rows show input stimuli, with linear velocity stimulation along the y-axis (magenta), OKS velocity around the z-axis (light green), and tilt angular velocity around the x-axis (cyan). Tilt angular velocity is 0 during this stimulation. The third and fourth rows from the top show the simulation results of horizontal eye velocity around the z-axis (red) and vertical eye velocity around the x-axis (blue). The bottom two rows show the simulation results of linear velocity along the x-, y-, and z-axes (dark gray, dark magenta, and light gray, respectively), and angular velocity around x, y, and z-axis (dark cyan, dark gray, and light gray, respectively), estimated by the Kalman filter. Eye movements and estimated self-motions traces show the average traces of the 12 simulation runs.

Figure 10

Results of our modified Kalman filter model simulation in response to roll-tilt head rotation in the dark. In the Kalman filter model, the process noise + passive stimuli standard deviation of interaural linear acceleration was set to a small value (0.001 G) at panel (A) and a large value (0.180 G) at panel (B) to reproduce roll-tilt test paradigms before and after training. The top two rows show input stimuli, with linear velocity stimulation along the y-axis (magenta) and tilt angular velocity around the x-axis (cyan). Linear velocity stimulation (magenta) is 0 during this stimulation. The third and fourth rows from the top show the simulation results of horizontal eye velocity around the z-axis (red) and vertical eye velocity around the x-axis (blue). The bottom two rows of panels show the simulation results of linear velocity along the x-, y-, and z-axes (dark gray, dark magenta, and light gray, respectively), and angular velocity around the x-, y-, and z-axes (dark cyan, dark gray, and light gray, respectively), estimated by the Kalman filter. Eye movements and estimated self-motions traces show the averaged traces of 12 simulation runs.