Mechanical characterization of regenerating Hydra tissue spheres

Abstract

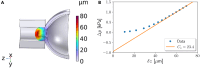
Hydra vulgaris, long known for its remarkable regenerative capabilities, is also a long-standing source of inspiration for models of spontaneous patterning. Recently it became clear that early patterning during Hydra regeneration is an integrated mechanochemical process whereby morphogen dynamics is influenced by tissue mechanics. One roadblock to understanding Hydra self-organization is our lack of knowledge about the mechanical properties of these organisms. In this study, we combined microfluidic developments to perform parallelized microaspiration rheological experiments and numerical simulations to characterize these mechanical properties. We found three different behaviors depending on the applied stresses: an elastic response, a viscoelastic response, and tissue rupture. Using models of deformable shells, we quantify their Young's modulus, shear viscosity, and the critical stresses required to switch between behaviors. Based on these experimental results, we propose a description of the tissue mechanics during normal regeneration. Our results provide a first step toward the development of original mechanochemical models of patterning grounded in quantitative experimental data.

Figure 1

Parallelized microaspiration experiments. (A) Schematic of the mold for the PDMS channel (details on dimensions can be found in Fig. S1). (B) Representation of the principle of the experiment. The insert, in orange, effectively creates an array of cylindrical tunnels, equivalent to model micropipettes. The tissue spheres, in yellow, flow toward these openings and, once sealed, are aspirated within. (C) Snapshot of a mounted channel with an insert containing ten tunnels in parallel. (D) Fluorescent imaging of the ectoderm of six samples aspirated within the tunnels. To see this figure in color, go online.

Figure 2

Elastic behavior quantification. (A) Snapshots of one tissue sphere aspirated in a hole at increasing pressure steps (top to bottom). The dashed red line shows the position of the aspirated tongue at each step, and L is the aspirated length. (B) Linear relationship between the applied pressure and $\delta z$ for a single tissue sphere and 10 different pressure steps showing both the linear behavior (fitted as a blue line) and negative intercept. (C) Same measurement as in (B), repeated on n = 36 tissue spheres, each represented by a differently colored line. (D) distribution of Young’s moduli obtained by this method. Black dots are individual measurements; the box plot shows the median and quartiles of the distribution. We found E = (4.4 ± 3.3) × 10² Pa (mean ± standard deviation, n = 36). To see this figure in color, go online.

Figure 3

Numerical simulations. (A) Graphical representation of the deformed shell. The color code represents the z-component of the displacement field. Black lines delineate the reference state of the system. Parameter values for these simulations are $R_0=160\mu \mathrm{m},h_0=20\mu \mathrm{m},E=440\text{Pa},\nu =0.495,\Delta P={10}^3\text{Pa}$. (B) applied pressure $\Delta p$ versus the displacement $\delta z$ for the same parameter values. The slope of the fitted line, in orange, corresponds to a value $C_S=23.4$. To see this figure in color, go online.

Figure 4

Viscoelastic flow at large applied pressure. (A) Snapshots of a tissue sphere showing flow at a constant applied pressure. (B) four examples of typical dynamics of the flow as a function of time. Dots of different colors represent four independent samples and solid lines fits by Eq. 8. (C) Distribution of measured viscosities as black dots . The box plot shows the median and quartiles of the distribution. We found it to be (2.4 ± 1.2) × 10⁶ Pa s (mean ± standard deviation, n = 22). To see this figure in color, go online.

Figure 5

Critical stresses between different mechanical behaviors. (A) Snapshot of an experiment showing two similar samples displaying different behaviors at the same applied pressure. (B) Quantification of the fraction of viscous behavior at different applied pressures. (C) Quantification of the fraction of samples showing tissue rupture as a function of applied pressure. In (B) and (C), dots are data and solid lines fit by a sigmoid function. In black are control samples and in red samples pretreated with 2 mM EDTA. Each point is derived from 18–40 samples stemming from eight different experiments in (B) and four in (C). (D) Numerical simulations. The color code represents the hoop stress within the aspirated shell when aspirated at a pressure of 1 kPa. Parameter values are the same as in Fig. 3. To see this figure in color, go online.