Stochastic Compartment Model with Mortality and Its Application to Epidemic Spreading in Complex Networks

Abstract

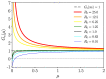
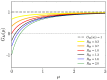
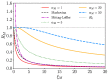
We study epidemic spreading in complex networks by a multiple random walker approach. Each walker performs an independent simple Markovian random walk on a complex undirected (ergodic) random graph where we focus on the Barabási-Albert (BA), Erdös-Rényi (ER), and Watts-Strogatz (WS) types. Both walkers and nodes can be either susceptible (S) or infected and infectious (I), representing their state of health. Susceptible nodes may be infected by visits of infected walkers, and susceptible walkers may be infected by visiting infected nodes. No direct transmission of the disease among walkers (or among nodes) is possible. This model mimics a large class of diseases such as Dengue and Malaria with the transmission of the disease via vectors (mosquitoes). Infected walkers may die during the time span of their infection, introducing an additional compartment D of dead walkers. Contrary to the walkers, there is no mortality of infected nodes. Infected nodes always recover from their infection after a random finite time span. This assumption is based on the observation that infectious vectors (mosquitoes) are not ill and do not die from the infection. The infectious time spans of nodes and walkers, and the survival times of infected walkers, are represented by independent random variables. We derive stochastic evolution equations for the mean-field compartmental populations with the mortality of walkers and delayed transitions among the compartments. From linear stability analysis, we derive the basic reproduction numbers RM,R0 with and without mortality, respectively, and prove that RM<R0. For RM,R0>1, the healthy state is unstable, whereas for zero mortality, a stable endemic equilibrium exists (independent of the initial conditions), which we obtained explicitly. We observed that the solutions of the random walk simulations in the considered networks agree well with the mean-field solutions for strongly connected graph topologies, whereas less well for weakly connected structures and for diseases with high mortality. Our model has applications beyond epidemic dynamics, for instance in the kinetics of chemical reactions, the propagation of contaminants, wood fires, and others.

Keywords: compartment model with mortality; epidemic spreading; memory effects; random graphs; random walks.

Figure 1

Left frame: Gamma distribution for four different cases: weakly singular (at $t=0$) [$\langle t\rangle =0.5$, $\xi =0.7$], exponential [$\langle t\rangle =2$, $\xi =0.5$], broad [$\langle t\rangle =1.5$, $\xi =4$], and narrow [$\langle t\rangle =1.5$, $\xi =30$]. Right frame: Their persistence (survival) probability distributions of Equation (27), where the same color code is used.

Figure 2

Endemic states of infected walkers/nodes $J_{w,n}(\infty )=(R_0-1)/(R_0+r)$ versus $R_0$ for various values of parameter r, which has to be read $r={\beta }_n\langle t_I^n\rangle$ ($r={\beta }_w\langle t_I^w\rangle$) for the walker’s (node’s) endemic states.

Figure 3

$G\left(\mu \right)$ of (39) for some Gamma-distributed $t_I^{w,n}$. Positive zeros of $G\left(\mu \right)$ exist only for $R_0>1$ (instability of globally healthy state).

Figure 4

$G_e\left(\mu \right)$ of (42) for different values of $R_0$, where $G_e\left(\mu \right)>0$ for $R_0>1$ (stability of the endemic state).

Figure 5

We depict function $G_M\left(\mu \right)$ of Equation (47) for a few values of $R_M$ for exponentially distributed $t_I^{w,n},t_M$. The basic reproduction number $R_M$ is monotonously decreasing with increasing mortality parameter ${\xi }_M$ (see Figure 6). The parameters are ${\beta }_{w,n}=1$, ${\alpha }_I^w=1$, ${\xi }_I^w=1$, ${\alpha }_n=1$, ${\xi }_I^n=0.5$ with $R_0=2$, where, here, $\langle t_{I,M}\rangle =R_0/(1+{\xi }_M)$.

Figure 6

Basic reproduction number $R_M$ of Equation (52) versus mortality rate parameter ${\xi }_M$ for Gamma-distributed $t_I^{w,n},t_M$ for various ${\alpha }_M$, where we have set ${\beta }_n={\beta }_w=\langle t_I^w\rangle =\langle t_I^n\rangle =1$, (${\alpha }_I^w={\xi }_I^w=0.3$) and ${\alpha }_M=1$, ${\alpha }_w={\xi }_I^w=1$ for the Markovian case, which is recovered by Equation (53).

Figure 7

Barabási–Albert, Erdös–Rényi, and Watts–Strogatz types with 300 nodes and connectivity parameters used in some of the simulations. The WS graph for connectivity parameter $m=2$ lacks the small-world property, resembling a complex real-world structure. The ER network has a broad degree distribution and the small-world property. The BA graph is for $N\to \infty$ asymptotically scale-free with a power law degree distribution and the small-world feature, where a large number of nodes have small degrees and, a few (hub) nodes, very large degrees. Almost all nodes are only a few links away from hub nodes.

Figure 8

Snapshots of spreading in a WS graph ($Z=2000$ walkers, $N=2000$ nodes, connectivity parameter $m=2$) and mortality parameter ${\xi }_M=0.4$ with $\mathcal{D}(\infty )\approx 16\%$. The average degree is $\langle k\rangle ={\sum }_{i=1}^N{k}_i/N=2$, here coinciding with connectivity parameter m. Other parameters are the same as in Figure 9. The upper frames show the evolution from the random walk data. One observes $d_w(\infty )\approx 0.99$ and $S_w(\infty )\approx 1\%$ with only about 20 surviving walkers after extinction of the disease. S walkers are drawn in cyan color; I walkers are in red; D walkers are invisible; nodes without walkers are represented in black. Consult here an animated video of this process https://drive.google.com/file/d/1-fhroAsoAVDKGR5H9yWtqjD7A1ZU5pQt/view (accessed on 22 April 2024).

Figure 9

The plots show the evolution on the WS graph with $Z=1000$ walkers for connectivity parameter $m=8$ (coinciding with the average degree) and rewiring probability $p=0.7$ ($nx.connected\_watts\_strogatz\_graph(N=1000,m=8,p=0.7)$) without mortality (left frame) and with mortality (right frame). $t_I^{w,n},t_M$ are Gamma-distributed with the parameters $\langle t_M\rangle =14$, ${\xi }_M=2$, $\langle t_I^w\rangle =8$, ${\xi }_I^w=10$, and $\langle t_I^n\rangle =15$, ${\xi }_n={10}^5$; see the histogram. The overall mortality $\mathcal{D}(\infty )\approx 1\%$ is the same as in Fig. Figure 10 and determined by the numerical integration of (7). The random walk data are generated by averaging over 50 random walk realizations.

Figure 10

Evolution on the WS graph with $Z=1000$ walkers and $N=1000$ nodes for the same parameters as in Figure 9 averaged over 50 random walk realizations, but with reduced connectivity parameter $m=\langle k\rangle =2$. The upper frame shows a snapshot ($t=15$) of the spreading in one random walk realization (susceptible walkers green, susceptible nodes black, infected nodes red).

Figure 11

Evolution on the ER graph ($nx.erdos\_renyi\_graph(N=1000,p=0.1)$) with $Z=1000$ walkers and small probability $p=0.1$ (above the percolation limit $p_c=0.01$ to ensure a connected structure). The parameters are $\langle t_I^n\rangle =5$, ${\xi }_I^n=10$, $\langle t_I^w\rangle =10$, ${\xi }_I^w=0.05$, $\langle t_M\rangle =65$, ${\xi }_M=1$. The average degree of this ER graph is very large with $\langle k\rangle =pN=100$.

Figure 12

Evolution on Barabási–Albert graph with $Z=50$ walkers and $N=5000$ nodes ($nx.barabasi\_albert\_graph(N=5000,m=5)$ and the average degree $\langle k\rangle \approx 10$) with parameters $\langle t_I^n\rangle =32$, ${\xi }_I^n={10}^4$, $\langle t_I^w\rangle =8$, ${\xi }_I^w={10}^4$ (sharp $t_I^{w,n}$), $t_M=500$, ${\xi }_M={10}^{-3}$. The basic reproduction number $R_M$ is here only slightly smaller than $R_0$ without mortality. The left upper frame shows the initial condition. S walkers are represented in blue, I walkers in red, and nodes in black. The random walk data are generated by averaging over 10 random walk realizations.

Figure 13

Evolution with the same parameters and number of walkers ($Z=50$) as in Figure 12, but fewer nodes ($N=2100$) for one random walk realization and average degree $\langle k\rangle \approx 9.98$. We interpret the increase of $R_M$ and $R_0$ due to more frequent passages of susceptible walkers on infected nodes (higher infection rates). Here, we performed only one random walk realization.