A Spectral Investigation of Criticality and Crossover Effects in Two and Three Dimensions: Short Timescales with Small Systems in Minute Random Matrices
- PMID: 38785644
- PMCID: PMC11119109
- DOI: 10.3390/e26050395
A Spectral Investigation of Criticality and Crossover Effects in Two and Three Dimensions: Short Timescales with Small Systems in Minute Random Matrices
Abstract
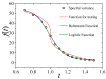
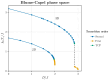
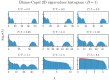
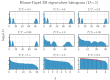
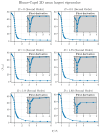
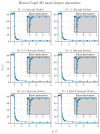
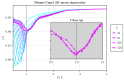
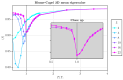
Random matrix theory, particularly using matrices akin to the Wishart ensemble, has proven successful in elucidating the thermodynamic characteristics of critical behavior in spin systems across varying interaction ranges. This paper explores the applicability of such methods in investigating critical phenomena and the crossover to tricritical points within the Blume-Capel model. Through an analysis of eigenvalue mean, dispersion, and extrema statistics, we demonstrate the efficacy of these spectral techniques in characterizing critical points in both two and three dimensions. Crucially, we propose a significant modification to this spectral approach, which emerges as a versatile tool for studying critical phenomena. Unlike traditional methods that eschew diagonalization, our method excels in handling short timescales and small system sizes, widening the scope of inquiry into critical behavior.
Keywords: Wishart matrix; crossover phenomena; phase transitions; random matrices.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
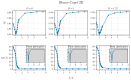
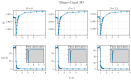
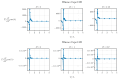



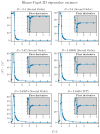
References
-
- Stanley H.E. Introduction to Phase Transitions and Critical Phenomena. Oxford Science Publications; Oxford, UK: 1987.
-
- Bouchaud J., Potters M. Theory of Financial Risk and Derivative Pricing. Cambridge University Press; Cambridge, UK: 2003.
-
- Castellano C., Fortunato S., Loreto V. Statistical physics of social dynamics. Rev. Mod. Phys. 2009;81:591–646. doi: 10.1103/RevModPhys.81.591. - DOI
-
- Szabo G., Fath G. Evolutionary games on graphs. Phys. Rep. 2007;446:97–216. doi: 10.1016/j.physrep.2007.04.004. - DOI
-
- Barabasi A.-L. Network Science. Cambridge University Press; Cambridge, UK: 2016.
Grants and funding
LinkOut - more resources
Full Text Sources

