Conservative significance testing of tripartite statistical relations in multivariate neural data
- PMID: 38800452
- PMCID: PMC11117094
- DOI: 10.1162/netn_a_00259
Conservative significance testing of tripartite statistical relations in multivariate neural data
Abstract
An important goal in systems neuroscience is to understand the structure of neuronal interactions, frequently approached by studying functional relations between recorded neuronal signals. Commonly used pairwise measures (e.g., correlation coefficient) offer limited insight, neither addressing the specificity of estimated neuronal interactions nor potential synergistic coupling between neuronal signals. Tripartite measures, such as partial correlation, variance partitioning, and partial information decomposition, address these questions by disentangling functional relations into interpretable information atoms (unique, redundant, and synergistic). Here, we apply these tripartite measures to simulated neuronal recordings to investigate their sensitivity to noise. We find that the considered measures are mostly accurate and specific for signals with noiseless sources but experience significant bias for noisy sources.We show that permutation testing of such measures results in high false positive rates even for small noise fractions and large data sizes. We present a conservative null hypothesis for significance testing of tripartite measures, which significantly decreases false positive rate at a tolerable expense of increasing false negative rate. We hope our study raises awareness about the potential pitfalls of significance testing and of interpretation of functional relations, offering both conceptual and practical advice.
Keywords: Functional connectivity; Multicollinearity; Partial information decomposition; Redundancy; Significance testing; Synergy.
Plain language summary
Tripartite functional relation measures enable the study of interesting effects in neural recordings, such as redundancy, functional connection specificity, and synergistic coupling. However, estimators of such relations are commonly validated using noiseless signals, whereas neural recordings typically contain noise. Here we systematically study the performance of tripartite estimators using simulated noisy neural signals. We demonstrate that permutation testing is not a robust procedure for inferring ground truth statistical relations from commonly used tripartite relation estimators. We develop an adjusted conservative testing procedure, reducing false positive rates of the studied estimators when applied to noisy data. Besides addressing significance testing, our results should aid in accurate interpretation of tripartite functional relations and functional connectivity.
© 2022 Massachusetts Institute of Technology.
Conflict of interest statement
Competing Interests: The authors have declared that no competing interests exist.
Figures

 ,
,  ,
,  ,
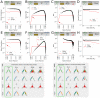
,  . The width of individual lines or triangles qualitatively indicates the magnitude of the effect. In this plot, all information atoms are shown with maximal magnitude for reference. (B) Example questions about tripartite relations that may be of interest in neuroscience. Left: Is the functional connection between X and Z specific with respect to the confounding variable Y? Middle: Are X, Y, and Z redundantly encoding the same information? Right: Could Z control synchronization between X and Y? (for example, if X and Y control forelimbs and hind limbs, respectively, and Z determines if the animal is currently running or resting). Note: the three sketches are made as a function of time for illustrative purposes only. In principle, information atoms can be computed across any data dimension. Here, we compute information atoms across trials.
. The width of individual lines or triangles qualitatively indicates the magnitude of the effect. In this plot, all information atoms are shown with maximal magnitude for reference. (B) Example questions about tripartite relations that may be of interest in neuroscience. Left: Is the functional connection between X and Z specific with respect to the confounding variable Y? Middle: Are X, Y, and Z redundantly encoding the same information? Right: Could Z control synchronization between X and Y? (for example, if X and Y control forelimbs and hind limbs, respectively, and Z determines if the animal is currently running or resting). Note: the three sketches are made as a function of time for illustrative purposes only. In principle, information atoms can be computed across any data dimension. Here, we compute information atoms across trials.





References
LinkOut - more resources
Full Text Sources
