Constraining functional coactivation with a cluster-based structural connectivity network

Abstract

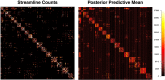
In this article, we propose a two-step pipeline to explore task-dependent functional coactivations of brain clusters with constraints from the structural connectivity network. In the first step, the pipeline employs a nonparametric Bayesian clustering method that can estimate the optimal number of clusters, cluster assignments of brain regions of interest (ROIs), and the strength of within- and between-cluster connections without any prior knowledge. In the second step, a factor analysis model is applied to functional data with factors defined as the obtained structural clusters and the factor structure informed by the structural network. The coactivations of ROIs and their clusters can be studied by correlations between factors, which can largely differ by ongoing cognitive task. We provide a simulation study to validate that the pipeline can recover the underlying structural and functional network. We also apply the proposed pipeline to empirical data to explore the structural network of ROIs obtained by the Gordon parcellation and study their functional coactivations across eight cognitive tasks and a resting-state condition.

Keywords: Chinese restaurant process; Diffusion tensor imaging; Factor analysis; Gordon parcellation; Structural and functional connectivity; fMRI.

Figure 1.

Two-step pipeline for structural and functional data analysis. An illustration with P = 9 ROIs and K = 3 clusters (3 ROIs per cluster). The first row describes the first step of the pipeline in which a nonparametric Bayesian clustering method is applied to the streamline counts matrix S. This produces a cluster assignment matrix Z, a cluster connectivity matrix ρ, and a binary ROI-to-ROI connectivity matrix G. The other rows illustrate the second step in which a factor analysis model is applied to a correlation matrix of fMRI data measured during different cognitive tasks (e.g., memory, attention, and learning tasks). This produces a factor-ROI loading matrix Λ, a factor correlation matrix Φ, and a uniqueness (the proportion of variance unexplained by factors) matrix Ψ. In the second step, factors are defined as the clusters from the first step and the factor structure is informed by the clustered structural network (i.e., Z informs the shape of Λ). Task-dependent coactivations of brain factors (clusters) are captured by differences in Φ matrices. See the Models section for a detailed description of the models in the pipeline.

Figure 2.

Two types of structural clusters. Adopted from Figure 2 in Hinne et al. (2015). The colored circles represent clusters, whereas the small black circles within the colored circles represent ROIs. Solid lines show within-cluster edges and dashed lines show between-cluster edges.

Figure 3.

Recovery of the connectivity matrix G. The top row shows the true, data-generating structural connectivity profile, whereas the bottom row shows the estimated recovery profile. We selected five plausible scenarios ranging from perfectly independent clusters (first column), representations of actual data (second column), completely randomly generated (third and fourth columns), and a single cluster (fifth column).

Figure 4.

Recovery of the cluster connectivity matrix ρ. The top row shows the true, data-generating connectivity profile, whereas the bottom shows the resulting estimate. We selected five plausible scenarios ranging from perfectly independent clusters (first column), representations of actual data (second column), and completely randomly generated (third and fourth columns). The scenario with a single cluster is not shown because ρ is not defined when there is only one cluster.

Figure 5.

Tile plots for the recovery of the factor loading matrix Λ. The top row shows the recovered factor loading matrix using exploratory factor analysis (EFA), whereas the bottom shows the results using confirmatory factor analysis (CFA). The columns correspond to the various conditions in our simulation study, where the first column shows the true, data-generating factor loading matrix.

Figure 6.

Scatterplots for the recovery of the factor loading matrix Λ. The estimated factor loading matrix value is shown against the true value used to generate the data for both exploratory factor analysis (EFA; red circles) and confirmatory factor analysis (CFA; blue squares) for each of the five conditions.

Figure 7.

Tile plots for the recovery of the factor correlation matrix Φ. The first row show the true, data-generating matrix, whereas the second and third rows show the estimates obtained using either exploratory factor analysis (EFA) or confirmatory factor analysis (CFA), respectively. Each of the columns corresponds to a particular condition used in the simulation study. For visual clarity, the cells in each matrix have been thresholded at 0.5 and color-coded according to the key on the right-hand side.

Figure 8.

Scatterplots for the recovery of the factor correlation matrix Φ. Each panel shows the estimated factor correlation matrix against the true data-generating value for each of the five conditions. In the Independent condition (first column), the estimates are shown as histograms because all of the true values were set to 0. In each panel, red corresponds to the estimate obtained using exploratory factor analysis (EFA) and blue corresponds to the estimate obtained using confirmatory factor analysis (CFA).

Figure 9.

Scatterplots for the recovery of the uniqueness matrix Ψ (diagonal entries). Each panel shows a scatterplot of the estimates obtained using exploratory factor analysis (EFA; red) or confirmatory factor analysis (CFA; blue) for each of the five conditions examined in the simulation study. In each panel, estimates are plotted on the x-axis, whereas the true data-generating values are shown on the y-axis.

Figure 10.

Empirical result: ROI connectivity matrix G and cluster connectivity matrix ρ. The top-left panel shows the estimated ROI connectivity matrix G. Within-cluster edges are color-coded to distinguish clusters, and between-cluster edges are colored black. White-coded cells indicate the absence of edges between ROIs. The bottom-left panel shows the estimated cluster connectivity matrix ρ. Intra- and intercluster connectivity values are color-coded according to the legend on the right-hand side of the panel. The right panel shows the network image of G. Nodes represent ROIs and gray lines represent edges between nodes. Node sizes are proportional to the surface areas of the ROIs. ROI nodes are color-coded according to the legend on the bottom-right side (as done for the top-left panel).

Figure 11.

Absolute model fit. The left panel shows the streamline count data matrix and the right shows a posterior predictive distribution generated by simulating the clustering model 1,000 times. Both matrices are color-coded according to the legend on the far-right side.

Figure 12.

Empirical result: Factor loading matrices of functional connectivity. Each row corresponds to a different randomly selected subject, whereas the columns correspond to a different task. In each panel, the estimated factor loading matrix is shown, where the elements are color-coded according to the key on the right-hand side.

Figure 13.

Empirical result: Factor loadings, cross loadings, and individual differences in factor correlations. The left panel shows the histograms of loadings (red) and cross loadings (gray), with the y-axis representing the densities. The middle panel shows the distribution of ∥Φ_Task − Φ_Rest∥_F across subjects, but separately by task (see the legend on the top-right side), which represents individual differences in functional coactivations by task. The right panel shows the histogram of the subject-wise standard deviations (SD) in mean correlation values across tasks, quantifying within-subject across-task differences. Φ_Task: Functional factor correlation matrix in a task. Φ_Rest: Functional factor correlation matrix in the resting-state. ∥A∥_F: Frobenius norm of a matrix A.

Figure 14.

Empirical result: Factor correlation matrices of functional connectivity. Each row corresponds to a different randomly selected subject, whereas the columns correspond to a different task. In each panel, the estimated factor correlation matrix is shown, where the elements are color-coded according to the key on the right-hand side.

Figure 15.

Absolute model fit. Comparison between the data correlation matrices (top row) and their corresponding implied (reproduced) correlation matrices (bottom row). Five pairs of subjects and conditions are selected for an illustration (columns).

Figure 16.

Absolute model fit. The left panel shows the scatterplot of data and predicted correlation values for 9 tasks and randomly selected 5 subjects. The lower triangular elements of the implied (reproduced) correlation matrix were plotted on the x-axis against the corresponding data correlation values. Correlations from different subjects were color-coded according to the legend on the top left and numbers 1–9 indicate different tasks (see below). The middle panel shows the histogram of the Pearson correlations between lower triangular elements of the data correlation matrix and their corresponding predictions across all 203 subjects and 9 tasks. The right panel shows the histograms of the root mean squared residuals (SRMR; red) and the root mean squared error of approximation (RMSEA; blue) across all 203 subjects and 9 tasks. The red and blue vertical lines indicate the upper bound criteria for a good fit for SRMR and RMSEA, respectively. Numbers in the left panel (tasks): 1 = Resting state, 2 = Affect, 3 = Empathy, 4 = Encoding, 5 = Go No-go, 6 = Retrieval, 7 = Reward, 8 = Theory of mind, 9 = Working memory.

Figure 17.

Functional-behavioral analysis. Each panel shows the lower diagonal entries of the functional factor correlation matrix Φ for the task shown on the top of the panel. The factor (cluster) numbers are shown on the rows and columns of each panel. The colored cells indicate the factor correlations that significantly predict performance measures. Those cells are color-coded according to the legend on the bottom of each panel. On the top-right side of each panel, the R-squared for the regression model only with the selected predictors is shown.