O-glycans Expand Lubricin and Attenuate Its Viscosity and Shear Thinning
- PMID: 38815979
- PMCID: PMC11238335
- DOI: 10.1021/acs.biomac.3c01348
O-glycans Expand Lubricin and Attenuate Its Viscosity and Shear Thinning
Abstract
Lubricin, an intrinsically disordered glycoprotein, plays a pivotal role in facilitating smooth movement and ensuring the enduring functionality of synovial joints. The central domain of this protein serves as a source of this excellent lubrication and is characterized by its highly glycosylated, negatively charged, and disordered structure. However, the influence of O-glycans on the viscosity of lubricin remains unclear. In this study, we employ molecular dynamics simulations in the absence and presence of shear, along with continuum simulations, to elucidate the intricate interplay between O-glycans and lubricin and the impact of O-glycans on lubricin's conformational properties and viscosity. We found the presence of O-glycans to induce a more extended conformation in fragments of the disordered region of lubricin. These O-glycans contribute to a reduction in solution viscosity but at the same time weaken shear thinning at high shear rates, compared to nonglycosylated systems with the same density. This effect is attributed to the steric and electrostatic repulsion between the fragments, which prevents their conglomeration and structuring. Our computational study yields a mechanistic mechanism underlying previous experimental observations of lubricin and paves the way to a more rational understanding of its function in the synovial fluid.
Conflict of interest statement
The authors declare no competing financial interest.
Figures

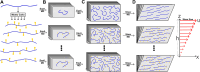

 . Initial (t = 0) and posterior
(t > 0) snapshots are shown, highlighting the
lubricin
fragments in blue. (E) Velocity profiles were obtained upon box deformation
under different shear rates. The line corresponds to the linear fit.
Output shear rates, i.e., u/h, are
shown in the legend. Also, the expected values of shear rates are
0.94, 0.625, 0.50, 0.25, 0.125, 0.06, and 0.03 ns–1.
. Initial (t = 0) and posterior
(t > 0) snapshots are shown, highlighting the
lubricin
fragments in blue. (E) Velocity profiles were obtained upon box deformation
under different shear rates. The line corresponds to the linear fit.
Output shear rates, i.e., u/h, are
shown in the legend. Also, the expected values of shear rates are
0.94, 0.625, 0.50, 0.25, 0.125, 0.06, and 0.03 ns–1.
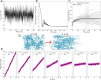
 obtained from equilibrium simulations
obtained from equilibrium simulations  and shear-driven NEMD simulations
and shear-driven NEMD simulations  . Five different systems were considered,
either without glycans (“w.o”: open symbols and dashed
or dotted lines) or with glycans (“w.”: closed symbols
and solid lines). Systems with medium (“w.”: green)
and high (“w.+”: orange) levels of glycosylation were
considered at the indicated mass (ρ) and molar densities (with N indicating the number of peptides in the system). A low-density
system without glycans was also simulated (blue). For systems where
zero shear Newtonian viscosities are available, fits to the Carreau
model (eq 6, a = 2) are shown (solid or dotted lines). Dashed lines are
fitted to a simple power law expression
. Five different systems were considered,
either without glycans (“w.o”: open symbols and dashed
or dotted lines) or with glycans (“w.”: closed symbols
and solid lines). Systems with medium (“w.”: green)
and high (“w.+”: orange) levels of glycosylation were
considered at the indicated mass (ρ) and molar densities (with N indicating the number of peptides in the system). A low-density
system without glycans was also simulated (blue). For systems where
zero shear Newtonian viscosities are available, fits to the Carreau
model (eq 6, a = 2) are shown (solid or dotted lines). Dashed lines are
fitted to a simple power law expression  without a Newtonian plateau. The viscosity
of water, both experimental and obtained here, is also displayed as
reference (gray and black, respectively). (B) Sample geometry for
Reynolds calculations with a flat wall sliding at velocity U against a parabolic height profile
without a Newtonian plateau. The viscosity
of water, both experimental and obtained here, is also displayed as
reference (gray and black, respectively). (B) Sample geometry for
Reynolds calculations with a flat wall sliding at velocity U against a parabolic height profile  with hmin =
50 nm, hmax = 10 μm, and Lx = 10 mm. (C) Pressure profiles
for lubricants with medium and high levels of glycosylation and three
different sliding velocities. At low speed, normalized pressure profiles
(by a reference pressure η0LU/h2) fall onto the same curve, indicating that
the flow is still in the Newtonian regime, as shown in the inset.
(D) Effect of shear thinning in the Reynolds calculations shown by
the local relative viscosity
with hmin =
50 nm, hmax = 10 μm, and Lx = 10 mm. (C) Pressure profiles
for lubricants with medium and high levels of glycosylation and three
different sliding velocities. At low speed, normalized pressure profiles
(by a reference pressure η0LU/h2) fall onto the same curve, indicating that
the flow is still in the Newtonian regime, as shown in the inset.
(D) Effect of shear thinning in the Reynolds calculations shown by
the local relative viscosity  along the sliding direction.
along the sliding direction.
 . Low values of Stot/∑Si indicate a high degree of protein aggregation,
whereas a value of one denotes zero aggregation. Symbols represent
data obtained from EMD simulations at zero shear rate and shear-driven
NEMD simulations at nonzero shear rates (average ± standard error, n = 4). Dashed lines correspond to nonglycosylated systems
(“w.o.”), while solid lines represent glycosylated ones
(medium glycosylated: “w.” and highly glycosylated:
“w.+”). Color indicates mass densities. The viscosity–shear
response (of Figure 5A) is shown at the top of A for comparison. (C,D) The ratio of viscosity
η(w.)/η(w.o.) is presented as a function of the ratio X(w.)/X(w.o.), with X = Rg (C) and X = Stot/∑Si (D), in both the medium (green)
and high (orange) mass density regimes. Correlation coefficients (r) for each data set are indicated. (E) Representative snapshots
for the extreme cases highlighted with arrows in A and B are shown
(backbone: blue and (un)glycosylated side chains: gray).
. Low values of Stot/∑Si indicate a high degree of protein aggregation,
whereas a value of one denotes zero aggregation. Symbols represent
data obtained from EMD simulations at zero shear rate and shear-driven
NEMD simulations at nonzero shear rates (average ± standard error, n = 4). Dashed lines correspond to nonglycosylated systems
(“w.o.”), while solid lines represent glycosylated ones
(medium glycosylated: “w.” and highly glycosylated:
“w.+”). Color indicates mass densities. The viscosity–shear
response (of Figure 5A) is shown at the top of A for comparison. (C,D) The ratio of viscosity
η(w.)/η(w.o.) is presented as a function of the ratio X(w.)/X(w.o.), with X = Rg (C) and X = Stot/∑Si (D), in both the medium (green)
and high (orange) mass density regimes. Correlation coefficients (r) for each data set are indicated. (E) Representative snapshots
for the extreme cases highlighted with arrows in A and B are shown
(backbone: blue and (un)glycosylated side chains: gray).
 . Symbols depict data obtained from the
simulations (average ± standard error, n = 4).
Dashed lines correspond to nonglycosylated systems (“w.o.”),
while solid lines represent glycosylated “w.” systems.
Colors indicate mass density. The viscosity–shear response
(of Figure 5A) is shown
at the top of B for comparison. (D,E) The ratio η(w.)/η(w.o.)
is presented as a function of the ratio X(w.)/X(w.o.), with X = NCFmax, i.e., the maximum of
the NCF, at short-range (C) and long-range (D) separations, in both
the medium (green) and high (orange) mass density regimes. Correlation
coefficients (r) for each data set are indicated.
. Symbols depict data obtained from the
simulations (average ± standard error, n = 4).
Dashed lines correspond to nonglycosylated systems (“w.o.”),
while solid lines represent glycosylated “w.” systems.
Colors indicate mass density. The viscosity–shear response
(of Figure 5A) is shown
at the top of B for comparison. (D,E) The ratio η(w.)/η(w.o.)
is presented as a function of the ratio X(w.)/X(w.o.), with X = NCFmax, i.e., the maximum of
the NCF, at short-range (C) and long-range (D) separations, in both
the medium (green) and high (orange) mass density regimes. Correlation
coefficients (r) for each data set are indicated.Similar articles
-
Characterisation of lubricin in synovial fluid from horses with osteoarthritis.Equine Vet J. 2017 Jan;49(1):116-123. doi: 10.1111/evj.12521. Epub 2015 Dec 16. Equine Vet J. 2017. PMID: 26507102
-
The O-glycomap of lubricin, a novel mucin responsible for joint lubrication, identified by site-specific glycopeptide analysis.Mol Cell Proteomics. 2014 Dec;13(12):3396-409. doi: 10.1074/mcp.M114.040865. Epub 2014 Sep 3. Mol Cell Proteomics. 2014. PMID: 25187573 Free PMC article.
-
Sialidase Unmasks Mucin Domain Epitopes of Lubricin.J Histochem Cytochem. 2016 Nov;64(11):647-668. doi: 10.1369/0022155416668139. Epub 2016 Sep 30. J Histochem Cytochem. 2016. PMID: 27680668 Free PMC article.
-
Lubrication of Articular Cartilage.Annu Rev Biomed Eng. 2016 Jul 11;18:235-58. doi: 10.1146/annurev-bioeng-081514-123305. Annu Rev Biomed Eng. 2016. PMID: 27420572 Review.
-
Rheological properties of synovial fluid due to viscosupplements: A review for osteoarthritis remedy.Comput Methods Programs Biomed. 2020 Nov;196:105644. doi: 10.1016/j.cmpb.2020.105644. Epub 2020 Jul 3. Comput Methods Programs Biomed. 2020. PMID: 32645531 Review.
Cited by
-
Lubricin's Mucin Domain Has Strong Polyproline Type-II Helical Character.bioRxiv [Preprint]. 2025 Jun 18:2025.06.15.659778. doi: 10.1101/2025.06.15.659778. bioRxiv. 2025. PMID: 40667325 Free PMC article. Preprint.
-
Breaking Down the Bottlebrush: Atomically Detailed Structural Dynamics of Mucins.J Chem Inf Model. 2024 Oct 28;64(20):7949-7965. doi: 10.1021/acs.jcim.4c00613. Epub 2024 Sep 27. J Chem Inf Model. 2024. PMID: 39327869 Free PMC article.
References
-
- Vakis A. I.; Yastrebov V. A.; Scheibert J.; Nicola L.; Dini D.; Minfray C.; Almqvist A.; Paggi M.; Lee S.; Limbert G.; et al. Modeling and simulation in tribology across scales: An overview. Tribol. Int. 2018, 125, 169–199. 10.1016/j.triboint.2018.02.005. - DOI
-
- Klein J. Molecular mechanisms of synovial joint lubrication. Proc. Inst. Mech. Eng., Part J 2006, 220, 691–710. 10.1243/13506501JET143. - DOI
-
- Gonzales G.; Zauscher S.; Varghese S. Progress in the design and synthesis of viscosupplements for articular joint lubrication. Curr. Opin. Colloid Interface Sci. 2023, 66, 101708.10.1016/j.cocis.2023.101708. - DOI
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

