The observation of π-shifts in the Little-Parks effect in 4Hb-TaS2

Abstract

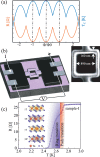
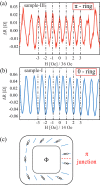
Finding evidence of non-trivial pairing states is one of the greatest experimental challenges in the field of unconventional superconductivity. Such evidence requires phase-sensitive probes susceptible to the internal structure of the order parameter. We report the measurement of the Little-Parks effect in the unconventional superconductor candidate 4Hb-TaS₂. In half of our rings, which are fabricated from single-crystals, we find a π-shift in the transition-temperature oscillations. According to theory, such a π-shift is only possible if the order parameter is non-s-wave. In the absence of crystallographic defects, the shift provides evidence of a multi-component order parameter. Thus, this observation increases the likelihood of the two-component order parameter scenario in 4Hb-TaS₂. Furthermore, we show that T_c is enhanced as a function of the out-of-plane field when a constant in-plane field is applied, which we explain using a two-component order-parameter.

Fig. 1. The Little–Parks experiment setup.

a The expected variation of the resistance and of the transition temperature as the flux through the ring is changed. Φ is the applied flux through the ring, and Φ₀ is the quantum flux. b A schematic description of the device. The purple layer represents the SiO_x layer of the substrate and the protective layer. The aluminum contacts are shown in gray, and the black layer is the 4Hb-TaS₂ flake. A scanning electron microscope image of a ring is shown. c The temperature dependence of the resistance of sample-I, a 1.1 × 1.1 μm² ring with 140 nm thickness. The colored regimes represent the transitions of the large pads and of the ring, which take place at slightly different temperatures. Inset: The unit cell of 4Hb-TaS₂.

Fig. 2. Little–Parks oscillations in 4Hb-TaS₂.

a Little–Parks oscillations for sample-II, a ring with a lateral size of 0.9 × 0.9 μm² and a thickness of 100 nm. The dashed red line is the fourth-order polynomial used for subtracting the background. b Same data as in a with the background subtracted. As many as 45 oscillations are measured in this ring. c Data for sample-I taken at T = 2.65 K (see R vs. T for the same sample in Fig. 1c). No oscillations are observed at this temperature. The minimum of the resistance in such curves is used to determine the absolute value of the field in the superconducting magnet. The dashed lines represent the magnetic field at which half of the oscillation period is found in this sample. d Temperature dependence of the Little–Parks oscillations from sample-I. The oscillations are observed only in a narrow temperature range.

Fig. 3. π-shift in the Little–Parks oscillations.

a The magnetoresistance of a π-ring. In these rings, the phase of the oscillations is shifted by π showing a resistance maximum at zero magnetic field. Data shown was measured at T = 2.35 K in a 0.575 μm² ring having a thickness of ~100 nm. b The magnetoresistance of a 0-ring, having a minimum at zero magnetic field. In both (a) and (b), the background was subtracted. c Possible explanation for the π shift in the Little–Parks oscillations: Strain fields (blue lines) align the two-component order parameter close to T_c. The strain field presented here realizes a half vortex. Consequently, the order parameter, schematically represented by the white and gray lobes, can not align with strain without developing a spontaneous π junction.

Fig. 4. Little–Parks oscillations in the presence of an in-plane magnetic field.

a Same ring as in Fig. 2a, measured in the presence of a 360 Oe in-plane magnetic field. The background has a “Mexican-hat” shape in this case, with minima at about ±80 Oe. b Resistance as a function of the out-of-plane field with the 360 Oe in-plane applied at a higher temperature of 2.66 K where the oscillations are absent. The parabolic background found in the absence of the in-plane field, as shown in Fig. 2c, is recovered. c Little–Parks oscillations in a π-ring without in-plane field. d Same π-ring measured in the presence of a 470 Oe in-plane magnetic field. In this case, the background has a minima at about ±150 Oe. e Theoretical calculation of ΔT_c/T_c for an annular ring with similar dimensions and a two-component order parameter. The magnetic field couples to the two-component order parameter linearly and causes the emergence of two maxima. For more details, see Supplementary material.