Simplifications and approximations in a single-gene circuit modeling

Abstract

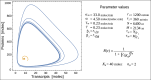
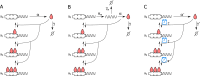
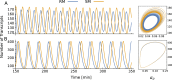
The absence of detailed knowledge about regulatory interactions makes the use of phenomenological assumptions mandatory in cell biology modeling. Furthermore, the challenges associated with the analysis of these models compel the implementation of mathematical approximations. However, the constraints these methods introduce to biological interpretation are sometimes neglected. Consequently, understanding these restrictions is a very important task for systems biology modeling. In this article, we examine the impact of such simplifications, taking the case of a single-gene autoinhibitory circuit; however, our conclusions are not limited solely to this instance. We demonstrate that models grounded in the same biological assumptions but described at varying levels of detail can lead to different outcomes, that is, different and contradictory phenotypes or behaviors. Indeed, incorporating specific molecular processes like translation and elongation into the model can introduce instabilities and oscillations not seen when these processes are assumed to be instantaneous. Furthermore, incorporating a detailed description of promoter dynamics, usually described by a phenomenological regulatory function, can lead to instability, depending on the cooperative binding mechanism that is acting. Consequently, although the use of a regulating function facilitates model analysis, it may mask relevant aspects of the system's behavior. In particular, we observe that the two cooperative binding mechanisms, both compatible with the same sigmoidal function, can lead to different phenotypes, such as transcriptional oscillations with different oscillation frequencies.

Figure 1

The sketches of autorepressive single-gene circuit from the perspective of three description levels. In model I the transcription and translation are described as instantaneous processes that occur at an average rate of ${\alpha }_m$ and $\alpha$, respectively (A). Model II includes the open state of DNA ($m_0$), and the translation initiation complex ($c_0$) (B). Model III considers the elongation processes associated with mRNA and proteins represented by boxes (C). Note that elongation processes can be mathematically described by a dedicated ODE for each step (Eq. 3) or by a set of differential equations with delays (Eq. 6). In three cases transcript and proteins are degraded following first-order reactions with rates ${\gamma }_m$ and $\gamma$, respectively. In all three cases, the transcription is regulated following a repressive Hill function.

Figure 2

The dynamics of a transcriptional oscillator from the perspective of three description levels. Trajectories in the phase plane for three models. The parameter values used in these simulations are the same values that were used in and are listed in the right panel. Model I has a stable fixed point (black dot), model II exhibits stable spiral behavior (yellow line), and model III exhibits sustainable oscillations (blue line). The initial conditions used for models I and II are $m_0(0)=1.0$ and $m(0)=c_0(0)=c(0)=0$. The initial conditions for delay model III are $m_0=1.0$ for $-\infty <t\le 0$, while m, $c_0$ and c are zero in such interval. The temporal range of the plot is from $50>t>500$. The effective elongation rates in model II have been written in terms of the single elongation step, as ${\beta }_1=r_1/N$ and ${\beta }_2=r_2/M$, where N and M denote the transcript and protein lengths.

Figure 3

Transcriptional regulatory functions for a repressor. The Hill function used in Fig. 2 ($K_d=40$ and $n_H=2$, black curve). Three Adair regulatory functions with different parameter values: $q=31.3$, $ϵ=5.5$ (blue curve), $q=43$, $ϵ=8.5$ (yellow curve), and $q=6.26$, $ϵ=5.5$ (green curve) and $p=0.1$ for all cases. The associated phenomenological parameters are $K_d=40$ $n_H=1.96$, $K_d=40.1$ $n_H=2.21$ and $K_d=8$, $n_H=1.96$, respectively (A). The same regulatory functions, but in the Hill plot style, where the vertical axis is the transformed receptor occupancy, i.e., $Log[\frac{R}{1-R}]$. This plot better demonstrates the difference between Hill and Adair’s regulatory functions. While the slope of a Hill function is constant and equal to the Hill coefficient $n_H$, this slope varies in the case of the Adair function (B).

Figure 4

Three autorepressive single-gene circuit models with explicit CRS dynamics. Model IV considers a CRS with three identical regulatory sites for FT that inhibit gene expression. The gene can only be expressed when the CRS has no bound TF. The TF expression occurs at an average rate of $\alpha$, and it is degraded at rate $\gamma$. (A). Model V is similar to the previous one, but the gene expression process is split into the transcription and translation steps as follows from Eq. (12) (B). Model III considers that the number of TFs regulating CRS is lagged due to the finite time consumed during processes such as translation, elongation, or translocation (C). In all three cases, the architecture of CRS is the same.

Figure 5

Temporal evolution of the single-gene circuit model corresponding to Eq. (14) with weak delay kernel for recruitment (blue line) and stabilization (magenta line) cooperative binding mechanisms, the weak distributed kernel function is depicted in the inset (A). Temporal evolution of Eq. (14), but with a strong delay kernel, the strong distributed kernel function is depicted in the inset (B). Temporal evolution of Eq. (14), but with a discrete delay, the inset depicts the trajectories in the phase plane (C). Parameter values: $p=0.246$, $q=30$, $ϵ=10$, ${\alpha }_m=33$, ${\gamma }_m=0.23$, $\alpha =4.5$, $\gamma =4.6$.

Figure 6

The effects of CRS dynamics on system stability. Time course and trajectories in the phase plane of a single-gene circuit model corresponding to Eq. (14) with a discrete delay kernel with different kinetic-factor values: $f=0.03$ (A), $f=0.06$ (B), and $f=0.09$ (C). The simulations are both for the recruitment (RM blue line) and stabilization (SM yellow line) cooperative binding mechanisms.

Figure 7

Time course and trajectories in the phase plane of single-gene circuit model corresponding to Eq. (14) with a discrete delay kernel with different kinetic-factor values: $f=1.5$ and $\tau =3.5$ (A), same f but $\tau =5.5$ (B). The simulations are both for the recruitment (blue line) and stabilization (yellow line) cooperative binding mechanisms.