A Randomized Parallel Algorithm for Efficiently Finding Near-Optimal Universal Hitting Sets
- PMID: 38835399
- PMCID: PMC11148856
- DOI: 10.1007/978-3-030-45257-5_3
A Randomized Parallel Algorithm for Efficiently Finding Near-Optimal Universal Hitting Sets
Abstract
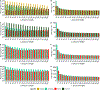
As the volume of next generation sequencing data increases, an urgent need for algorithms to efficiently process the data arises. Universal hitting sets (UHS) were recently introduced as an alternative to the central idea of minimizers in sequence analysis with the hopes that they could more efficiently address common tasks such as computing hash functions for read overlap, sparse suffix arrays, and Bloom filters. A UHS is a set of -mers that hit every sequence of length , and can thus serve as indices to -long sequences. Unfortunately, methods for computing small UHSs are not yet practical for real-world sequencing instances due to their serial and deterministic nature, which leads to long runtimes and high memory demands when handling typical values of (e.g. ). To address this bottleneck, we present two algorithmic innovations to significantly decrease runtime while keeping memory usage low: (i) we leverage advanced theoretical and architectural techniques to parallelize and decrease memory usage in calculating -mer hitting numbers; and (ii) we build upon techniques from randomized Set Cover to select universal -mers much faster. We implemented these innovations in PASHA, the first randomized parallel algorithm for generating nearoptimal UHSs, which newly handles . We demonstrate empirically that PASHA produces sets only slightly larger than those of serial deterministic algorithms; moreover, the set size is provably guaranteed to be within a small constant factor of the optimal size. PASHA's runtime and memory-usage improvements are orders of magnitude faster than the current best algorithms. We expect our newly-practical construction of UHSs to be adopted in many high-throughput sequence analysis pipelines.
Keywords: Parallelization; Randomization; Universal hitting sets.
Figures

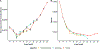
References
-
- Berger B, Rompel J, Shor PW: Efficient NC algorithms for set cover with applications to learning and geometry. J. Comput. Syst. Sci 49(3), 454–477 (1994)
-
- DeBlasio D, Gbosibo F, Kingsford C, Marçais G.: Practical universal k-mer sets for minimizer schemes. In: Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, pp. 167–176. ACM (2019)
-
- Deorowicz S, Kokot M, Grabowski S, Debudaj-Grabysz A: KMC 2: fast and resource-frugal k-mer counting. Bioinformatics 31(10), 1569–1576 (2015) - PubMed
-
- Johnson DS: Approximation algorithms for combinatorial problems. J. Comput. Syst. Sci 9(3), 256–278 (1974)
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
Miscellaneous
